zadania rozszerzone qwe: Prosiłbym o dokładne rozwiązanie całego zadania (od początku do końca) 1. Punkty P,Q,R są środkami boków kolejno AB,BC,CD równoległoboku ABCD. Wyznacz współrzędne wierzchołków równoległoboku, jeśli: a) P(2;0), Q(7;4), R(4;4) → → b) BA = [−5;5], BC = [2;4], Q(3; −1) → c) AB = [8;2], Q(7;2), R(6;4) → → 2. Przekątne AC i BD równoległoboku ABCD przecinają się w punkcie P(2;1). Jeśli (wektor)AC=[8;10] i (wektor)BD=[−6;8], to jeden z wierzchołków równoległoboku ma współrzędne? A. (5;−3) B. (7;4) C. (−2;4) D. (−4;−3) 3.Podstawa AB trapezu ABCD jest 3 razy dłuższa od podstawy CD. Mając dane A(1;2), (wektor)AD=[1;3], (wektor) DB = [5;0], oblicz współrzędne pozostałych wierzchołków trapezu 4. Dane są równania prostych zawierających dwie środkowe trójkąta: y=2 i y=−x+3 oraz jeden z jego wierzchołków: (1;−2). Wyznacz współrzędne środków boków tego trójkąta.

PW: Którego?

daras: chyba mamy wylosować

qwe: No wszystkie jeśli można

daras: nie można

J: 1) a) porównujesz wektory: PR = [2,4] BC = [x_c − x_b, y_c − y_b] ,czyli: x_c − x_b = 2 oraz y_c − y_b = 4

	xc + xb		yc + yb
a ponadto:		= 7 oraz		= 4
	2		2

z układu równań obliczysz: x_b, y_b , x_c , y_c ...potam prosto współrzędna A i D

qwe: @J dziękuję za to jedno @Daras... to po cholerę się udzielasz jeśli nie chcesz pomóc?

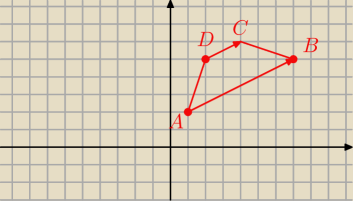
Janek191: z.3 D = A + [ 1; 3 ] = ( 1; 2) + [ 1; 3] = ( 2; 5) → DB = [5; 0 ] B = ( 2; 5) + [ 5; 0 ] = ( 7; 5) → AB = [ 7 − 1; 5 − 2] = [ 6 ; 3] → DC = ¹₃*[ 6; 3 ] = [ 2; 1] C = D + [ 2; 1] = ( 2; 5) + [ 2; 1] = ( 4; 6) Odp. B = ( 7; 5) , C = ( 4; 6) , D = ( 2; 5)

daras: @1q6:24 bo nie lubię leni

qwe: @Janek191 dziękuję

qwe: 1. Punkty P,Q,R są środkami boków kolejno AB,BC,CD równoległoboku ABCD. Wyznacz współrzędne wierzchołków równoległoboku, jeśli: → → b) BA = [−5;5], BC = [2;4], Q(3; −1) → c) AB = [8;2], Q(7;2), R(6;4)

qwe: Prosiłbym o to zadanie które wkleiłem wyżej (2 podpunkty) i o 2 oraz 4 jeszcze

PW: Mogę czwarte. Proste y = 2 i y = −x+ 3 przecinają się w punkcie (1, 2) (trzeba rozwiązać układ równań,ale że łatwy, to w pamięci). Jak wiadomo wszystkie środkowe przecinają się w tym punkcie (również ta trzecia której nie znamy przecina się w punkcie (1, 2) z tymi znanymi). Wiadomo również, że środkowe trójkąta są podzielone przez ich punkt wspólny − każda w stosunku 2:1 licząc od wierzchołka. W tym wypadku mamy informację: punkt A = (1, −2) (wierzchołek trójkąta) i punkt M = (1, 2) (wspólny punkt środkowych)

	2
wyznaczają odcinek, który stanowi		odcinka AD, gdzie D = (xD, yD) oznacza środek boku
	3

BC. Wobec tego

	2
		|AD| = |AM|
	3

	2		2
		(xD−1) = 1 − 1 i		(yD − (−2)) = 2 − (−2)
	3		3

	2		2
		(xD−1) = 0 i		(yD − (−2)) = 4
	3		3

x_D = 1 i y_D = 4. Jeden środek boku mamy: D = (1, 4). Można było to wyznaczyć łatwiej (oba punkty A i M leżą przypadkowo na prostej y = 1), ale idzie o metodę. Dalej myślimy tak: punkt D należy do prostej BC. Jeżeli prosta BC ma równanie y = ax+b, to 4 = a·1 + b, skąd a = 4 − b. czyli równanie prostej BC ma postać (1) y = (4−b)x + b. Należy dobrać tak parametr b, żeby punkty wspólne prostej (1) i środkowych y = 2 i y= − x + 3, czyli punkty B i C były końcami odcinka o środku D. Szczegóły nudne, więc zostawiam je pytającemu.

qwe: Dziękuję Ci bardzo