moduły Agatha: Jak rozwiązać 3x−|2−x|>0 Mam wątpliwości czy mam dobrze.

ZKS: Zamieść swoje rozwiązanie jeżeli chcesz wiedzieć, czy masz dobrze.

Agatha: 1. x należy do (−∞,2) I wychodzi mi x>1/2 uwzgl. założenia x należy (−1/2,2)

Agatha: +1/2 ma byc

Agatha: 2. x należy do <2,∞) i wychodzi x>−1/2 uwzgl założenia xnależy do <2,∞)

Agatha: a potem uwzgl 1 i 2 to wychodzi x nalezy do (1/2, 2)

ZKS: Bierze sumę 1^o oraz 2^o, nie część wspólną. W przypadku 2^o coś jest źle.

Agatha: w 2. jest x>−1 poprawiłam

Agatha: aha czyli na koniec trzeba sumę, a myślałam że część wspólną, czyli będzie: od (1/2 do∞)

Agatha: dobrze?

ZKS: Dobrze.

Mila: 3x−|2−x|>0⇔ 3x−|x−2|>0 1) |x−2|=x−2 dla x≥2 wtedy masz nierówność : 3x−(x−2)>0⇔ 3x−x+2>0 2x>−2 x>−1 i x≥2⇔x≥2 lub 2) |x−2|=−(x−2) =−x+2 dla x<2 wtedy masz nierówność: 3x−(−x+2)>0 3x+x−2>0 4x>2⇔

	1		1
x>		i x<2⇔x∊(		,2)
	2		2

Złączenie zbiorów

	1
x∊(		,∞)
	2

========

pigor: ..., albo np. tak : 3x−{2−x} >0 ⇔ 3x >{2−x| ⇔ |x−2|< 3x /² i x>0 ⇔ ⇔ x²+4−4x < 9x² i (*) x >0 ⇔ 2x²+x−1 >0 ⇔ 2x²−x+2x−1 >0 ⇔ ⇔ x(2x−1)+1(2x−1) >0 ⇔ 2(x−¹₂)(x+1) >0, stąd i z (*) ⇔ x∊(¹₂;+∞).

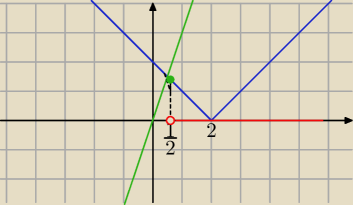
Eta: |2−x|= |x−2| 3x−|x−2|>0 ⇔ |x−2| <3x

	1
f(x)= |x−2| , g(x)= 3x (punkt wspólny wykresów |x−2|=3x ⇒ x=
	2

to f(x)<g(x) dla x∊(¹₂, ∞)