Aksjomaty i kombinatoryka MysteriousCore: Wiadomo, że zdarzenia A i B są niezależne, P(A−B) = 1/8 i P(B−A) = 3/8 Wykaż, że P(A∪B) = 7/8 lub P(A∪B) = 5/8 I mam mały problem i potrzebuje pomocy Pozwoliłem sobie rozpisać trochę powyższe rzeczy: P(A)−P(A∩B)=1/8 ⇒ P(A) = 1/8 + P(A∩B) ⇒ 1/8 + P(A)P(B) P(B)−P(A∩B)=3/8 ⇒ P(B) = 3/8 + P(A∩B) ⇒ 3/8 + P(A)P(B) Z racji że są niezależne można wnioskować, że P(A∩B) = P(A)*P(B) I teraz wzór na sumę: P(A∪B)=P(A)+P(B)−P(A∩B) ⇒ P(A)+P(B)−P(A)P(B) I co dalej bo kombinuje w różne strony ale nie chce dojść do dowodu...

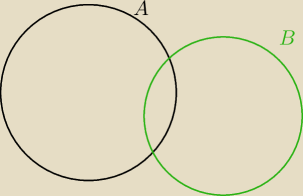
sushi_gg6397228: zrób sobie rysunek

MysteriousCore: Kurczę tylko pytanie jak ten rysunek będzie wyglądał

sushi_gg6397228:

MysteriousCore: Czyli jednak dobrze narysowałem i jeśli dobrze rozumieć A bez części wspólnej z B ma 1/8, natomiast B bez części wspólnej ma 3/8?

sushi_gg6397228: do części wspólnej dajesz "x" P(A∩B) = P(A)*P(B) −−> masz równanie kwadratowe, Δ, itp

Bogdan: Oznaczmy: P(A) = x, P(Y) = y

	1		3
x =		+ xy i y =		+ xy wystarczy rozwiązać ten układ równań
	8		8

	1		1		1		3
otrzymamy: x =		i y =		lub x =		i y =
	4		2		2		4

i potem obliczyć: P(A∪B) = x + y − xy