pochodne
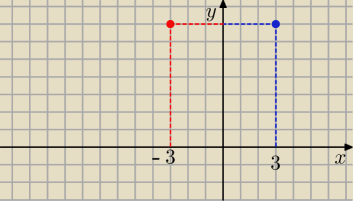
olaaa: Przyjmijmy, że wykres funckji f jest symetryczny względem osi y i f'(3)=7. Oblicz f'(−3).
Wiadomo, ze bedzie to −7 tylko jak to zapisac?

15 paź 19:47
olaaa: w sensie jak zapisac obliczenia?
15 paź 19:48
Janek191:
f( 3) = 7
f ( − 3) = f(3) = 7
15 paź 19:53
olaaa: to jest pochodna, a nie wartosc funkcji
15 paź 19:55
Janek191:
Nie zauważyłem " prima"

f '(3) = 7
15 paź 19:58
ICSP: f(x) − funkcja parzysta : f(x) = f(−x)
f'(x) = [f(−x)]' = −f(−x) − funkcja nieparzysta.
Wniosek : Pochodna funkcji parzystej jest funkcją nieparzystą.
15 paź 19:58
olaaa: f'(−3) to na pewno nie bedzie 7 tylko −7

Nie wiem tylko jak to "ladnie obliczyc"
wystarczy wlasnosc tgα=−tg(180−α)?
15 paź 20:01
ICSP: oj zgubiłem prima :
f'(x) = −f'(−x)

Oczywiście równość zachodzi tylko gdy f jest parzysta

15 paź 20:02
olaaa: dziekuje!

15 paź 20:20

 f( 3) = 7
f ( − 3) = f(3) = 7
f( 3) = 7
f ( − 3) = f(3) = 7
 f '(3) = 7
f '(3) = 7
 Nie wiem tylko jak to "ladnie obliczyc"
wystarczy wlasnosc tgα=−tg(180−α)?
Nie wiem tylko jak to "ladnie obliczyc"
wystarczy wlasnosc tgα=−tg(180−α)?
 Oczywiście równość zachodzi tylko gdy f jest parzysta
Oczywiście równość zachodzi tylko gdy f jest parzysta 
