liczby zespolone - interpretacja na wykresie tony67: Cześć! Chciałbym zapytać o kwestię zaznaczenia na wykresie nierówności, gdzie jest np.: Im(z⁶) >= 0 Z należy do zbioru liczb zespolonych. Czy w tej sytuacji biorąc część urojoną (a + bi)⁶ zostaje b⁶, więc czy zbiór na wykresie będzie wyglądał jak dla b²? W sensie tak samo jak dla x² >=0 dla każdego wartości w R przyjmie wartości dodatnie?

J: Im(z⁶) ≥ 0 ⇔ Im [r⁶(cos6α + isin6α] ≥ 0 ⇔ r⁶sin6α ≥ 0 ⇔ sin6α ≥ 0 teraz poszukaj przedziały ...na rysunku to otwarte obszary kątowe ( te przedziały )

tony67: Bardzo dziękuję za podpowiedź. 1. Czy wykorzystanie wcześniejsze b⁶ jest nadużyciem ze względu na brak określenia czym to b jest? 2. Czy dla rozwiąznia z sin6α >= 0 mogę to rozwiązanie określic jako: x >= (π/3) * n, gdzie n jest całkowite oraz x <= 1/6(2π*n +π) 3. Czy dla przykladu typu z⁸ czy z⁴ jest dokladnie taki sam tok rozumowania?

J: 1) skąd u Ciebie: Im[(a+bi)⁶] = b⁶ ? 2) rozwiązujesz zwyłą nierówność trygonometryczną w przedziale [0, 2π] 3) tak

tony67: 1. Fakt, przepraszam. To bez sensu. 2. W takim razie zawsze próbować ze wzoru de Moivre’a, aby nie utknąć w kosmicznych potęgach? Czyli np. dla prostszego przypadku z z⁴ byłoby to sin4α > =0 Czy mogę rozwiązać to w ten sposób, że 4α = k*pi, gdzie k jest całkowite Zatem α = 1/4(k*pi) Dziękuję.

J: sin6x ≥ 0 ⇔ 0 + 2kπ ≤ 6x ≤ π + 2kπ ⇔

	1		π		1
		kπ ≤ x ≤		+		kπ
	3		6		3

..... teraz podstawiwj kolejno: k= 0,1,2.... dopóki utrzymasz się w przedziale [0,2π] (prawdopodobnie 6 przedziałów ) ... potem rysunek

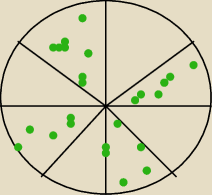
tony67: Przepraszam, nie umiem za bardzo rysowac tutaj, ale czy na wykresie wyglądałoby tak jak tutaj? Zielone kropki to "zakreskowana przestrzeń"... Czy jest jakieś narzędzie do rysowania tego online?

J: Masz dostać 6 przedziałów: 1) k = 0

	π		π
0 ≤ x ≤		→ x ∊ [0,		]
	6		6

2) k = 1

π		π		π		π		π		π
	≤ x ≤		+		=		→ x ∊ [		,		]
3		6		3		2		3		2

i tak dalej , aż do k = 5 ( w sumie otrzymasz 6 przedziałów )

tony67: Przepraszam za zamieszanie. Tamten rysunek odniósł się akurat do przykładu z z⁴, gdzie ten zaznaczony kąt miał w przybliżeniu oddać na rysunku 45 stopni. Chcąc narysować ten przykład w WolframAlpha: http://www.wolframalpha.com/input/?i=Plot3D%5BIm%5B%28a+%2B+I+b%29%5E6%5D%5D Uzyskuje się jasne i ciemne przedziały: http://www4f.wolframalpha.com/Calculate/MSP/MSP765320fc21c4i6fhf33b00003f130ebg8d06dgah?MSPStoreType=image/gif&s=20&w=300.&h=293.&cdf=RangeControl Z czego to wynika? Czy jasne przedziały to właśnie to jak powinien wyglądać ten rysunek?

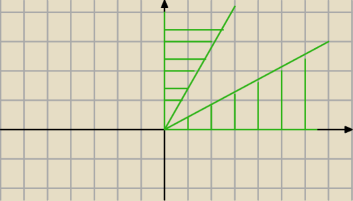
J: Tutaj masz dwa pierwsze przedziały ( oczywiście te proste idą do nieskończoności )

J: W Woframie te jaśniejsze przedziały ( jest ich 6 ) to właśnie rozwiąznie

tony67: Bardzo dziękuję, to oczywiście rozumiem. Chciałem po prostu sprawdzić gdzieś cały rysunek. Przy nieco trudniejszym przykładzie spotkałem z takim problemem, że: 1/6 π ≤ arg(−iz) ≤ 1/3 π Mam na myśli dwie kwestie: 1. Jeżeli jest samo arg(z) to na wykresie ograniczam jedno ramię poprzez kąt (tutaj 1/6 pi) zaś drugie ramię kąt 1/3 pi i wtedy to wszystko? 2. Jeżeli pod arg mam inne wyrazenie (−iz) to jak to wtedy interpretować?

J: 1) tak

	π
2) korzystamy ze wzoru: arg(−i*z) = arg(−1) + arg(z) + 2kπ = −		+ arg(z) + 2kπ
	2

J:

	π
literówka: arg(−i*z) = arg(−i) + arg(z) + 2kπ = −		+ arg(z) + 2kπ
	2

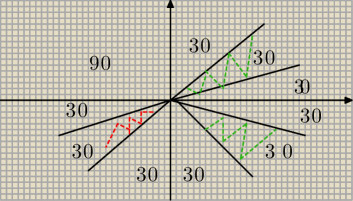
tony67: 2) Czyli tak dla takiego przykładu: 1/6 π ≤ arg(−iz) ≤ 1/3 π Czyli zgodnie ze wzorem (dla k =1) arg(z) + 3/2 pi Czyli jeden kat miedzy 1/6 pi a 1/3 pi, a drugi 5/3 pi a 11/6 pi? Mam na myśli zamalowaną zieloną część

J:

π		π		π		π		π
	≤ arg(−iz) ≤		⇒		≤ −		+ arg(z) ≤		⇒
6		3		6		2		3

π		π		π		π
	+		≤ arg(z) ≤		+
6		2		3		2

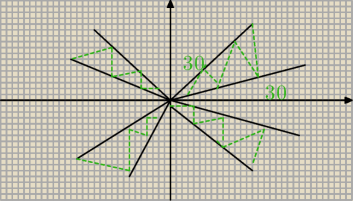
tony67: Dziękuję. Czy jeśli rysuję ogólne rozwiązanie powinien ująć wszystkie (w tym wypadku 4) kąty? W sensie wyglądałoby to tak Pierwszy: 30 − 60 stopni Drugi: 120 − 150 stopni Trzeci: 210 − 240 Czwaty: 300 − 330

J: a skąd masz 4 przedziały ?

tony67: Chodziło mi o kwestię tego 2 kπ. Czy powinienem zaznaczać wszystkie przedziały jeśli mam tu do dyspozycji 2 pi na rysunku? Dla k = 0 mam tak dwa przedziały zgodnie ze wskazówka. Czwarty przedział wychodził mi dla k = 1 Z tym trzecim chyba rzeczywiście przesadziłem. W sensie nie ma takiej opcji, żeby uzyskać z tego wzoru 7/12 pi (210 stopni) oraz 2/3 pi (240 stopni).

J: Masz przedział: <120⁰,150⁰> ... przecież jeśli dodasz 360⁰ to wyjdziesz poza 2π Ten przedział to tzw argument główny liczby zespolonej ( czyli należący do <0,2π> )

tony67: Rozumiem. Dziękuję raz jeszcze.