:) olekturbo:

	1
wyznacz przedziały monotoniczności w f(x) =
	x2−4

PW : Za pomocą pochodnej, czy elementarnie?

olekturbo: pochodnej pochodna to

x2−4−2x
(x2−4)2

f'(x) > 0 ⇔ x²−2x−4 i dalej rozwizac i bedzie dobrze?

olekturbo: i PW: takie pytanie x³−3x−m = 0 kiedy takie wyrażenie ma 3 pierwiastki?

Janek191:

	0*(x2 − 4) − 1*( 2 x)		− 2 x
f '(x) =		=
	( x2 − 4)2		(x2 − 4)2

PW : Źle pochodna. Licznik jest stałą, jego pochodna to zero.

PW : Oczywiście Janek191 mnie wyprzedził z korektą

olekturbo: ajj no tak zapomniałem. dziękuje moglibyscie mi pomóc z drugim zagadnieniem?

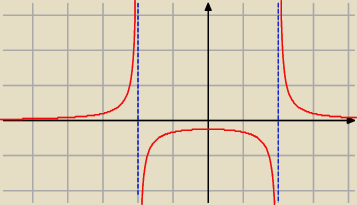
Janek191: x ≠ − 2 i x ≠ 2 f '(x) > 0 dla x < 0 i f '(x) < 0 dla x > 0 f '(0) = 0 f rośnie w ( − ∞ ; − 2) , ( − 2; 0) a maleje w ( 0; 2) , ( 2; +∞) f w punkcie x = 0 osiąga maksimum lokalne Patrz wykres

olekturbo: dziekuje

olekturbo: kompletnie zapomniałem

PW : h(x) = x³ − 3x ma trzy miejsca zerowe, umiesz je policzyć i narysować wykres − jakie ma maksimum i minimum lokalne. Co będzie, gdy wykres pociągniemy wzdłuż osi OY o −m?

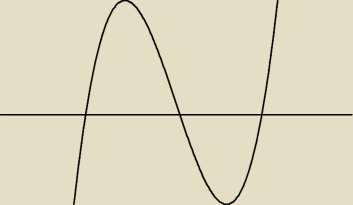
olekturbo: dla x = −1 jest maksimum lokalne y = 2 dla x = 1 jest minimum lokalne −2 wykres spadnie w dol?

olekturbo: to będzie mial trzy miejsca dla m ∊ (−2,2) bo w innym razie bedzie mial 2 miejsca zerowe?

PW : Jesteś blisko.

olekturbo: f'(x) = 3x²−3 f'(x) > 0 ⇔ x²−1 > 0 (x−1)(x+1) > 0 dla x = −1 y_max = 2−m dla x = 1 y_min = −2−m to zeby byly 3 rozwiazania, jedno ekstremum musi byc ujemne, wiec (2−m)(−2−m) < 0 −4+2m−2m+m² < 0 m²−4<0 (m−2)(m+2)<0 m ∊ (−2,2) dobrze zrozumialem chyba