równanie Niezdara: Dane jest równanie z parametrem m ∊ R |5x−2m|= |x+3m| Dla jakich wartości parametru m równanie posiada dokładnie jedno rozwiązanie? Jak wyjść z wartości bezwzględnych?

Niezdara: Podpowie ktos?

PW : Może wystarczy porysować "dzióbki"?

Niezdara: Rozważyć to dla 4 przypadków?

PW : Wykres takiego czegoś f(x) = |ax + b| to "dzióbek". Narysuj dwa i się zadumaj.

Niezdara: Jak mam to narysować przecież mam parametr? Wiem jak funkcja wyglada po nalozeniu wartosci bezwzglednej

PW : No ciężko pomóc. Narysuj dwa jakiekolwiek "dzióbki". Przecież masz równanie − muszą się przeciąć, żeby było rozwiązanie. Narysuj u siebie, tutaj nie trzeba.

Niezdara: No dobrze ale z tego mi nic dalej nie wynika.

PW : To przeczytaj jeszcze raz treść zadania. W ilu miejscach mają się przeciąć?

Niezdara: Graficznie wychodzi to jasne.

PW : ... że "dzióbki" mają stać ...

olekturbo:

PW : Skasowałeś kolegę?

olekturbo: ?

PW : Przecież "dzióbek" musi być nad osią OX (z wyjątkiem tego jednego punktu, w którym "stoi".

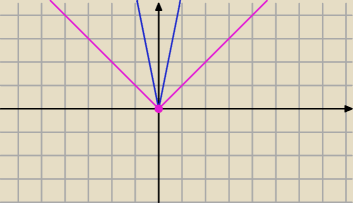
Eta: |5x−2m|=|x+3m| |²⇔ 25x²−20mx+4m²=x²+6mx+9m² 24x²−14mx−5m² =0 ma jedno rozwiązanie gdy Δ=0 Δ =196m²+480m²=0 ⇒ m=0 f(x)= |5x| i g(x)= |x| wspólnym punktem jest (0,0)

pigor: ..., dane jest równanie z parametrem m∊R : |5x−2m|= |x+3m| . Dla jakich wartości m równanie posiada dokładnie jedno rozwiązanie? −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− |5x−2m|=|x+3m| /² ⇔ (5x−2m)²= (x+3m)² ⇔ ⇔ 25x²+4m²−20mx−x²−9m²−6mx= 0 ⇔ ⇔ 24x²−26mx−5m²=0 i równanie to równoważne danemu ma dokładnie jedno rozwiązanie ⇔ Δ=0 ⇔ ⇔(26m)²+4*24*5m²=0 ⇔ 676m²+480m²=1156m²=0 ⇔ m=0 .

pigor: ..., ups; przepraszam, ale ... przysypiałem, stąd ...

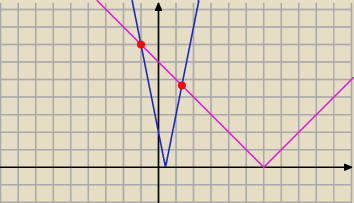
Eta: A no tak źle przeniosłam ( zamiast − 6mx sorry odp m=0 zgadza się wykresy obydwu funkcji nie mają równoległych "ramion" więc jedno rozwiązanie jest gdy przecinają się w "dzióbku" ( jak pisał PW tylko w punkcie (0,0) np: na rys ( wtedy miały by 2 punkty wspólne)

mario: Dziekuje bardzo !