Zespolone Benny: Oblicz:

	√3−i		i−√3		i(1+√3)+1−√3
b)4√		=4√		=4√		no i coś mi nie wychodzi
	−1−i		i+1		2

jak chce obliczyć pierwiastki.

Eta: Cierpliwości .....zaraz Mili wyjdzie

Benny: albo może inaczej, jak wychodzi cosinus bądź sinus bardzo dziwny to jak obliczać pierwiastki tego typu?

ZKS: Może skorzystaj ze wzoru łatwiej będzie liczyć.

z1		r1
	=		[cos(φ1 − φ2) + isin(φ1 − φ2)], gdzie r = |z|.
z2		r2

Benny: Myślałem o tym, ale będzie tu trochę liczenia, bo trzeba będzie policzyć 8 w_k.

ZKS: Dlaczego, aż osiem?

	7		7
zk = [2cos(		π) + i sin(		π)]1/4
	12		12

Benny: Inaczej sobie pomyślałem

Benny: Btw. przed nawiasem nie powinno być √2?

Benny:

	2
Mam obliczyć 6√(2−i)6, liczę sobie moduł z 2−i, i wychodzi mi √5, ale cosφ=		. Jak
	√5

wyznaczyć z tego φ?

Benny:

Benny:

	2√5		−√5		√5
cosφ=		, sinφ=		⇒ w0=		(2√5−√5i) jak policzyć kolejne
	5		5		5

pierwiastki znając pierwszy?

Benny:

ZKS: z = ⁶√(2 − i)⁶ Mamy od razu pierwszy pierwiastek z_o = 2 − i, kolejne liczymy przemnażając pierwszy

	k * 2π		k * 2π
pierwiastek przez cos(		) + isin(		).
	6		6

	π		π
z1 = (2 − i)[cos(		) + isin(		)]
	3		3

Mila: k∊{1,2,3,4,5}

ZKS:

Mila:

Benny: Masakra, a ja się tak męczyłem i wymyślałem jakieś dziwne rzeczy

Mila: Zapamiętaj wzór (16:14) podany przez ZKS, bardzo się przydaje.

Benny: No właśnie, gdzieś już go widziałem, ale musiałem kombinować oczywiście

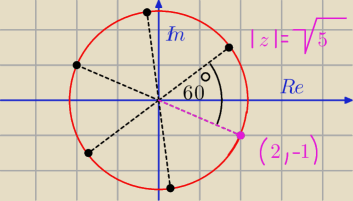
ZKS: Jak wiesz pierwiastki rozkładają się na okręgu równomiernie. Mamy pierwiastek stopnia szóstego, zatem 360^o należy podzielić przez 6, wychodzi nam 60^o, więc co 60^o mamy następny pierwiastek, stąd to się wzięło po prostu.

Benny: No w sumie to fakt To kolejne:

	z+i		π
arg		=
	z−i		2

Takich równań jeszcze nie rozwiązywałem, więc nie wiem od czego nawet zacząć.

Benny:

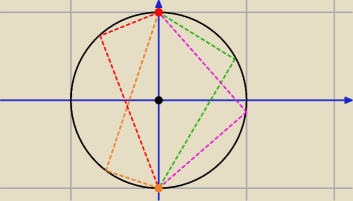
ZKS: Nie wiem, czy jest to poprawny sposób, ale mam taki pomysł.

	z + i		π
arg(		) =
	z − i		2

z₁ = z + i = x + (y + 1)i z₂ = z − i = x + (y − 1)i

	π
arg(z + i) − arg(z − i) =
	2

	π
φ1 − φ2 =
	2

	π
ctg(φ1 − φ2) = ctg(		)
	2

ctg(φ1)ctg(φ2) + 1
	= 0
ctg(φ2) − ctg(φ1)

ctg(φ₁)ctg(φ₂) + 1 = 0

	x
ctg(φ1) =
	y + 1

	x
ctg(φ2) =
	y − 1

x		x
	•		= −1
y + 1		y − 1

x2
	= −1
y2 − 1

x² = 1 − y² x² + y² = 1

Benny: Na ćwiczeniach zrobiliśmy to tak:

x+i(y+1)
	no i to przez sprzężenie i redukowanie wychodzi:
x+i(y−1)

x2+y2−1+2ix
x2+(y−1)2

No i założenia: x²+(y−1)²≠0 ⇒ x≠0 i y≠1 x²+y²=1

	π
x≥0, jak dobrze pamiętam to dlatego, że dla kąta		współczynnik przy "i" musi być
	2

nieujemny. i wychodzi półokrąg w 1 i 4 ćwiartce bez punktu (0;1) Jak patrze to Twoje rozwiązanie też jest dobre, ale brak w nim założeń.

ZKS: U mnie tego typu zadań nie było niestety, więc taki mi wpadł pierwszy lepszy pomysł. Dając pewnie odpowiednie założenia powinno wyjść to samo tak mi się wydaje.

Mila:

	π
arg(z+i)−arg(z−i)=
	2

	π
arg(x+(y+1)i)−arg(x+(y−1)i)=
	2

x≠0, y≠1

	x
cosφ1=
	√x2+(y+1)2

	y+1
sinφ1=
	√x2+(y+1)2

	x
cosφ2=
	√x2+(y−1)2

	y−1
sinφ2=
	√x2+(y−1)2

======================== cos(φ₁−φ₂)=0 sin(φ₁−φ₂)=1 cos(φ₁−φ₂)=cosφ₁*cosφ₂+sinφ₁*sinφ₂=0⇔

x		x		y+1		y−1
	*		+		*		=0⇔
√x2+(y+1)2		√x2+(y−1)2		√x2+(y+1)2		√x2+(y−1)2

x²+y²=1 Rozwiń drugi wzór i otrzymasz warunek na x.

Benny: