..
the.end: dane sa zbiory A={(x,y)∊R2 : x2=y+4}, B={(x,y)∊R2 : y=ax+b}, gdzie a,b ∊R. wskaż wszystkie
wartosci parametrów a,b, dla których zbiór A∩B jest:
a)pusty
b)jednelementowy
c)nieskończony
13 paź 19:39
sushi_gg6397228:
umiesz narysować zbiór A ?
13 paź 21:23
x: ja też mam to zadanie
to będzie parabola z miejscami zerowymi 2 i −2
13 paź 21:31
x: jedno elementowy, to będzie tylko kiedy styka się z wierzchołkiem

niby potrafię sobie wyobrazić inne miejsca jednoelementowe,
ale nie wydaje mi się żebym potrafiła to w jakiś logiczny sposób zapisać..
13 paź 21:32
sushi_gg6397228:
to robisz rysunek
13 paź 21:32
sushi_gg6397228:
akurat są funkcje, więc proste x= liczba odpadają
13 paź 21:34
x:
nie jestem pewna, czy potrafie rysować tutaj..
13 paź 21:39
x: jej, zanim to dodałam, to przypominało to parabole
13 paź 21:40
x: no tak ale y=ax+b to nie będzie prosta?
13 paź 21:40
sushi_gg6397228:
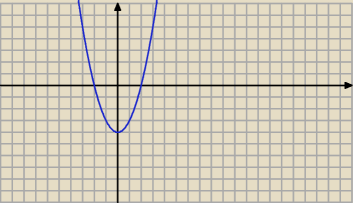
masz rysunek
potem zaznaczasz "kratkę " obok S , klikasz na obszar, potem przesuwasz mysz i drugi raz klik
−−> masz szarą szachownice
w pole wpisujesz wzór i klikasz w kratkę obok
13 paź 21:43
Admin:
13 paź 21:44
x:
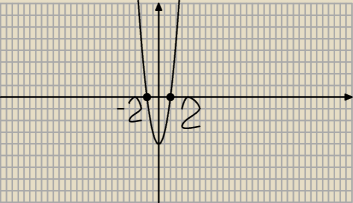
mam nadzieje, że teraz będzie lepiej, i dziękuję te instrukcje

13 paź 21:47
Eta:
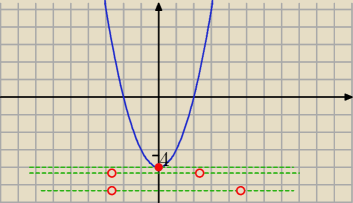
a) a=0 b<−4 np y= −5 lub y= −2016 ........
b) a=0 b=.....
c) ..........
13 paź 21:47
sushi_gg6397228:
masz kolory, wiec mozesz wybrac kolor i potem ikona wykresu, itp
klikasz kolor przed rysunkiem
szare kratki mozna zrobić większe , jak zrobisz symetrycznie, to nie trzeba pisać 2 i "−2", bo
każdy sobie policzy tak jak u mnie
13 paź 21:49
x: b) a=0 b=−4
c) a=0 b>−4
a co w przypadku gdzy a≠0..?
13 paź 21:50
sushi_gg6397228:
jak a jest liczbą to wykres jest ukośną kreską
13 paź 21:52
x:
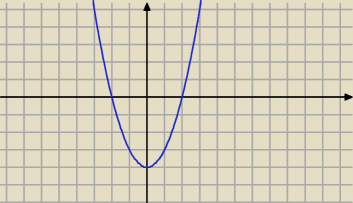
teraz lepiej

13 paź 21:53
sushi_gg6397228:
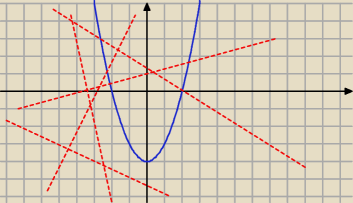
13 paź 21:53
x: no wiem, ale jak wtedy ropatrzyć te przypadki gdy a≠0?
13 paź 21:54
sushi_gg6397228:
jest zabawa, bo moga być ukośne, jak ta z lewej i tez nie ma punkty wspołnego z parabolą
13 paź 21:57
x: hmm, a te współczynniki a we wzorach ax2 +bx + c i ax +bx+c nie będą w jakiś sposób
równoważne
przy określaniu z jaką pędkością funkcję liniowa i kwadratowa rosną?
13 paź 22:04
sushi_gg6397228:
masz tabelke, wiec wpisz wzory np y= x−5 ; y= 2x +..., y= 0,5 x + ...
( i daj rózne kolory) i sobie rysuj i kasuj funkcje
13 paź 22:07
x:
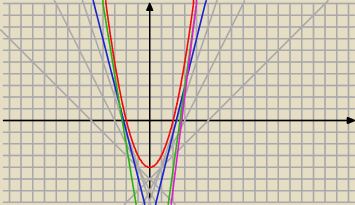
no to mam coś takiego:
a=1 lub a=−1 b≤−5
a=2 lub a=−2 b≤−6
a=3 lub a=−3 b≤−7
a=4 lub a=−4 b≤−9
a=5 lub a=−5 b≤−12
.. przy 8 będzie −22 itd
no to cuś takiego mi wyszło .. chyba się zadowole a =0
13 paź 22:23
misiek:
ups, oczom nie wierzę...
" a mogłaby nie być liczbą


?
Kreski to chyba po 3 piffku ....
13 paź 22:24
misiek:
a gdyby tak rozpatrzyć układ równań i ustalić liczbę rozwiązań
w zależności od parametrów a i b ?
13 paź 22:26
x: wybacz, dopiero uczę się rysować..
masz jakiś lepszy sposób na to?

13 paź 22:26
Eta:
 misiek
misiek jadłeś sushi ? i piłeś

?
13 paź 22:27
x: no to ma jakiś sens..
na mnie nie patrz, sushi tu zaproponował kasację przypadków

13 paź 22:27
misiek:
o metodzie kasacji w matematyce ierwszy raz słyszę

13 paź 22:30
misiek:
kresek to tutaj nie widzę, raczej parabolę i proste...
13 paź 22:31
misiek:
A={(x,y)∊R2 : x2=y+4}, B={(x,y)∊R2 : y=ax+b}
y=x2−4 i y=ax+b
x2−4=ax+b
x2−ax−4−b=0
Δ=a2+16+4b
zbiór jednoelementowy gdy a2+16+4b=0
13 paź 22:36
x: to jak rozpisać ten układ równań?
to Ty pierszy nazwałeś te proste kreskami

13 paź 22:36
x: o dzięki

13 paź 22:37
misiek: zbiór pusty gdy a2+16a+4<0
zbiór nieskończony ...nie ma takiej możliwości
13 paź 22:38
misiek:
POST: 21.52... do wglądu
13 paź 22:41
x: dlaczego nie ma możliwośći na zbiór nieskończony?
13 paź 22:42
x: racja, sushi był pierwszy z kreskami

13 paź 22:43
misiek:
prosta i parabola musiały by mieć nieskończenie wiele punktów wspólnych,
a maksymalnie mają dwa punkty wspólne
13 paź 22:45
misia:
Pozdrowienia dla
miśka 
13 paź 22:47
x: aha czyli opcja a=0 i b>−4 i nie będzie podchodzić pod c)nieskończenie wiele
bo ma tylko 2 punkty wspólne, to wiele zmienia,
13 paź 22:49
x: o już zejdźcie z sushi, wcześniej mi pomagał w zadaniach i całkiem dobrze to wychodziło
a propo twojego edytowanego posta misia
13 paź 22:51
Eta:
Dlaczego kasujesz posty? .......... M
13 paź 23:05
Mila:
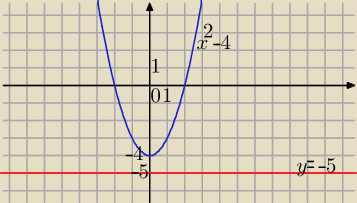
A={(x,y)∊R
2 : x
2=y+4}, B={(x,y)∊R
2 : y=ax+b}
y=x
2−4
y=ax+b
a) zbiór pusty⇔parabola i prosta nie maja punktów wspólnych
Zatem prosta y=ax+b jest równoległa do OX i leży poniżej wierzchołka paraboli.⇔
a=0 i b<−4
y=x
2 i y=0*x+b, gdzie b<−4
np.
y=x
2−4 i y=−5
I to koniec.
b) Tylko prosta równoległa do OX i przechodząca przez wierzchołek paraboli
ma dokładnie jeden punkt wspólny z parabolą⇔
a=0 i b=−4
czyli prosta
y=−4
c) Nie istnieje prosta, która ma nieskończenie wiele punktów wspólnych z parabolą.
13 paź 23:07
Eta:

13 paź 23:08
misiek:
dlaczego opis dotyczy tylko prostych poziomych ?
13 paź 23:12
misiek:
y=x2−4 oraz y=2x−5 mają jeden punkt wspólny
13 paź 23:16
Mila:
Masz rację.
Trzeba uzupełnić. Zapomniałam o stycznych.
Tak , jeszcze dochodzą styczne i proste pionowe: x=c, c∊R
Coś się wymyśli.
13 paź 23:33
misiek:
pionowe już nie, bo y=ax+b
13 paź 23:35
Eta:
x=c −− nie jest funkcją

13 paź 23:43
misiek: y=x2−4
y=ax+b
a) zbiór pusty⇔parabola i prosta nie maja punktów wspólnych
a2+16a+4b<0
b) a2+16a+4b=0
c) Nie istnieje prosta, która ma nieskończenie wiele punktów wspólnych z parabolą.
13 paź 23:44
Mila:
b)
1) a=0 i b=−4 styczna pozioma
c.d wykorzystamy Δ
2) a≠0
Δ=a
2+16+4b
a
2+16+4b=0
a
2+16=−4b
| | −1 | |
b= |
| a2−4 dla każdego b∊paraboli , gdzie zmienną niezależną jest a. |
| | 4 | |
Posprawdzaj, bo może mam jakiś błąd.
Czy to już będzie wszystko?
Etaaa?
13 paź 23:45
Eta:
taaak
brakuje jeszcze:
===================

13 paź 23:48
Mila:
x=c jest prostą, nie uwzględnioną w równaniu kierunkowym, które tu Cię obowiązują,
Napisałam, że takie proste mają jeden punkt wspólny.
13 paź 23:49
Mila:
To dobranoc, może wrócimy jeszcze jutro do tego ciekawego zadanka.

13 paź 23:50
Eta:

13 paź 23:51
misiek:
tak myślę, że nie trzeba rozgraniczać a =0 i a≠0.
13 paź 23:51
misiek: Dobranoc
13 paź 23:52
Mila:
Tam komentarz trzeba poprawić.
13 paź 23:53
 niby potrafię sobie wyobrazić inne miejsca jednoelementowe,
ale nie wydaje mi się żebym potrafiła to w jakiś logiczny sposób zapisać..
niby potrafię sobie wyobrazić inne miejsca jednoelementowe,
ale nie wydaje mi się żebym potrafiła to w jakiś logiczny sposób zapisać..
 nie jestem pewna, czy potrafie rysować tutaj..
nie jestem pewna, czy potrafie rysować tutaj..
 masz rysunek
potem zaznaczasz "kratkę " obok S , klikasz na obszar, potem przesuwasz mysz i drugi raz klik
−−> masz szarą szachownice
w pole wpisujesz wzór i klikasz w kratkę obok
masz rysunek
potem zaznaczasz "kratkę " obok S , klikasz na obszar, potem przesuwasz mysz i drugi raz klik
−−> masz szarą szachownice
w pole wpisujesz wzór i klikasz w kratkę obok
 mam nadzieje, że teraz będzie lepiej, i dziękuję te instrukcje
mam nadzieje, że teraz będzie lepiej, i dziękuję te instrukcje 
 a) a=0 b<−4 np y= −5 lub y= −2016 ........
b) a=0 b=.....
c) ..........
a) a=0 b<−4 np y= −5 lub y= −2016 ........
b) a=0 b=.....
c) ..........
 teraz lepiej
teraz lepiej 

 no to mam coś takiego:
a=1 lub a=−1 b≤−5
a=2 lub a=−2 b≤−6
a=3 lub a=−3 b≤−7
a=4 lub a=−4 b≤−9
a=5 lub a=−5 b≤−12
.. przy 8 będzie −22 itd
no to cuś takiego mi wyszło .. chyba się zadowole a =0
no to mam coś takiego:
a=1 lub a=−1 b≤−5
a=2 lub a=−2 b≤−6
a=3 lub a=−3 b≤−7
a=4 lub a=−4 b≤−9
a=5 lub a=−5 b≤−12
.. przy 8 będzie −22 itd
no to cuś takiego mi wyszło .. chyba się zadowole a =0

 ?
Kreski to chyba po 3 piffku ....
?
Kreski to chyba po 3 piffku ....

 misiek jadłeś sushi ? i piłeś
misiek jadłeś sushi ? i piłeś  ?
?






 A={(x,y)∊R2 : x2=y+4}, B={(x,y)∊R2 : y=ax+b}
y=x2−4
y=ax+b
a) zbiór pusty⇔parabola i prosta nie maja punktów wspólnych
Zatem prosta y=ax+b jest równoległa do OX i leży poniżej wierzchołka paraboli.⇔
a=0 i b<−4
y=x2 i y=0*x+b, gdzie b<−4
np.
y=x2−4 i y=−5
I to koniec.
b) Tylko prosta równoległa do OX i przechodząca przez wierzchołek paraboli
ma dokładnie jeden punkt wspólny z parabolą⇔
a=0 i b=−4
czyli prosta
y=−4
c) Nie istnieje prosta, która ma nieskończenie wiele punktów wspólnych z parabolą.
A={(x,y)∊R2 : x2=y+4}, B={(x,y)∊R2 : y=ax+b}
y=x2−4
y=ax+b
a) zbiór pusty⇔parabola i prosta nie maja punktów wspólnych
Zatem prosta y=ax+b jest równoległa do OX i leży poniżej wierzchołka paraboli.⇔
a=0 i b<−4
y=x2 i y=0*x+b, gdzie b<−4
np.
y=x2−4 i y=−5
I to koniec.
b) Tylko prosta równoległa do OX i przechodząca przez wierzchołek paraboli
ma dokładnie jeden punkt wspólny z parabolą⇔
a=0 i b=−4
czyli prosta
y=−4
c) Nie istnieje prosta, która ma nieskończenie wiele punktów wspólnych z parabolą.




