pochodna lotka:

	x3
Wyznacz przedziały monotoniczności i ekstrema lokalne funkcji f(x)=
	3−x2

lotka:

	9x2−x4
f'(x)=
	(3−x2)2

f'(x)=0 ⇔x≠{ −√3 ; √3 } i 9x²−x⁴=0 ⇒x należy {−3;0;3}

lotka: Ktoś wie co dalej?

Janek191:

	x3
f(x) =		, x ≠ − √3 i x ≠ √3
	3 − x2

	3 x2*(3 − x2) − x3*(−2 x)		9x2 − 3x4 +2 x4
f ' (x) =		=		=
	(3 − x2)2		(3 − x2)2

	9x2 −x4		x2*(9 −x2)
=		=		= 0 ⇔ x = 0 lub x = − 3 lub x = 3
	(3 −x2)2		(3 − x2)2

W x = − 3 f' zmienia znak z − na + ( minimum lokalne ) W x = 0 f ' nie zmienia znaku ( punkt przegięcia ) W x = 3 f ' zmienia znak z + na − ( maksimum lokalne )

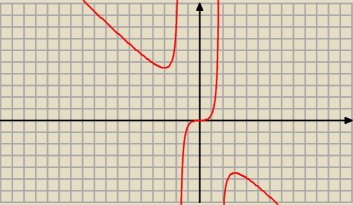Janek191: Patrz wykres

lotka: Dziękuję Janek191