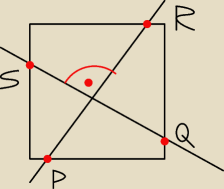
wykaż x: wykazać że jeśli proste prPR i prSQ są prostopadłe to |PR|=|SQ| jakieś wskazówki, z jaką bronią się za to zabrać?

x: ktoś coś?

x: jakieś pomysły?

x: a jak by przedłużyć te proste i z talesa?

5-latek: Jeśli to jest kwadat to mysle nad przystawaniem trojkatow Oznaczyc punkt przecięcia się prostych i badac cechy przystawania .

x: to jest kwadrat, przepraszam nie napisałam wcześniej z tym przytawiem, to już nie pierwszy dzień się główkuję, ale niestety nic tu nie widzę

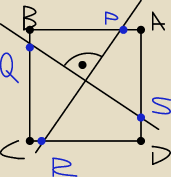
x: Punkty P,Q,R,S leżą odpowiednio na bokach AB, BC, CD i DA pewnego kwadratu. Wykazać, że jeśli pr PR i pr SQ są prostopadłe, to |PR|=|SQ|

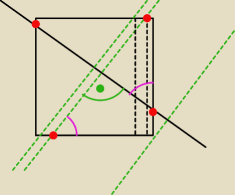
henrys: może ten rysunek Cię naprowadzi

5-latek: Witaj Dziekuje , będę myslal

henrys: Witaj, witaj, powinno pójść gładko

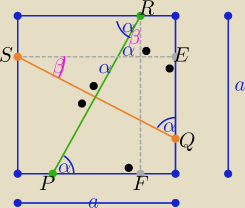
Eta: α+β=90^o ΔPFR≡ ΔQSE z cechy ( kbk) |RF|=|SE|=a i |∡PRf|=|∡QSE|=β i |∡SEQ|= |∡PFR|=90^o zatem |PR|=|SQ|

x: dzięki za pomoc

5-latek: Dobry wieczor Eta dziekuje za pokazanie rozwiązania .

5-latek: A tak sobie mysle teraz ze u kolegi Henrysia trzeba będzie rozpatrzyć dwie proste rownolegle przeciet trzecia prosta i rozpatrzyć odpowiednie katy

henrys: nieeee 5−latku , ten rysunek miał pokazać, że niezależnie jak poprowadzimy tą prostą prostopadłą do pierwszej, długość odcinka PR się nie zmieni, zaznaczyłem takie same kąty, rozumowanie to samo

5-latek: Dobrze czytam teraz o prostych równoległych i tak mi jakos utkwilo w pamięci

henrys: nie będę wam zabierał radości z myślenia nad geometrią