Równania i nierówności wykładnicze
van: Wyznacz wszystkie wartości parametru m (m∊R) dla których równanie
3
2x−2(m−1)*3
x+m+5=0 ma jedno rozwiązanie
Proszę o pomoc

, policzyłem tylko z założenia że Δ=0 i wyszło mi m
1=−1 m
2=4 i nie wiem co
dalej zrobić... poprawna odp to m∊(−
∞,−5)∪{4}
12 paź 21:18
ICSP: sam warunek Δ = 0 jest niewystarczajacy. Brakuje też warunków gdy Δ ≥ 0
12 paź 21:19
van: mógłbyś/mogłabyś wytłumaczyć ? Bo z mojego rozumowania to przy Δ≥0 mam już 2 rozwiązania...
12 paź 21:21
ICSP: t = 3x
założmy, że dostaniesz rozwiązania t1 = 1 oraz t2 = −1. Ile będzie wtedy wartości x ?
12 paź 21:22
van: Nie mam pojęcia...
Δt dała mi wynik 4m2−12m−16
Δm dała m1=−1 i m2=4 i nie wiem co dalej z tym robić. :c
12 paź 21:26
olekturbo: t > 0
12 paź 21:27
olekturbo: t1t2 > 0
t1+t2 > 0
12 paź 21:28
ICSP: Inaczej:
W liczbach rzeczywistych rozwiaż równanie:
3x = −1
12 paź 21:28
van: ?
12 paź 21:29
van: 3x=−1
3x=1−1
i dalej mój mózg nie widzi możliwości
12 paź 21:31
5-latek:
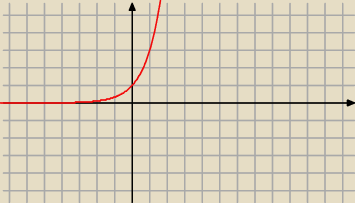
To jest wykres funkcji y=3
x . jakie wartości ona przyjmuje ?
12 paź 21:32
ICSP:
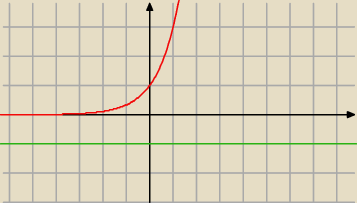
12 paź 21:33
van: no dodatnie
12 paź 21:33
van: no więc x=−1
wtedy 3x=−1
12 paź 21:36
ICSP: no to skoro funkcja wykładnicza f(x) = 3x przyjmuje wartości tylko dodatnie to ile rozwiązań
będzie miało równanie : 3x = −1 ?
12 paź 21:37
van: jedno
12 paź 21:39
ICSP: nie
12 paź 21:40
van: ale my schodzimy z zadania kompletnie. na co mi rozwiązanie 3x=−1 skoro ja mam równanie w
którym nie wiem dlaczego musze zakładać że Δ≥0 i co mam dalej robić z wyliczonymi parametrami
m !
12 paź 21:41
ICSP: Właśnie nie schodzimy z zadania. Równanie 3x = −1 jest równaniem sprzecznym. Zatem, jeżeli
twoje równanie : t2 −2(m−1)t + m + 5 = 0 będzie miało dwa różne pierwiastki rzeczywiste
takie, że jeden z nich będzie dodatni a drugi ujemy to wtedy równanie 32x − 2(m−1)3x + m +
5 = 0 będzie miało tylko jeden pierwiastek:
t1 > 0
t2 < 0
3x = t1 − istnieje rozwiązanie
3x = t2 − równanie sprzeczne
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
łącznie 1 rozwiazanie.
12 paź 21:46
van: ale rozwiązaniem ma być przedział m∊(−∞,−5)∪{4}
12 paź 22:00
ICSP: Może warunki bardziej do Ciebie przemówią :
1o Δ > 0 i t1t2 < 0
2o Δ = 0 i t0 > 0
Koniunkcja tych warunków będzie odpowiedzią.
12 paź 22:11
 , policzyłem tylko z założenia że Δ=0 i wyszło mi m1=−1 m2=4 i nie wiem co
dalej zrobić... poprawna odp to m∊(−∞,−5)∪{4}
, policzyłem tylko z założenia że Δ=0 i wyszło mi m1=−1 m2=4 i nie wiem co
dalej zrobić... poprawna odp to m∊(−∞,−5)∪{4}
 To jest wykres funkcji y=3x . jakie wartości ona przyjmuje ?
To jest wykres funkcji y=3x . jakie wartości ona przyjmuje ?
