Planimetria-Geometria
Marw: Witam mam problem z 5 zadaniami kompletnie nie wiem jak je rozwiązać, a potrzebuję je zrobić na
jutro.
1.Oblicz obwód trapezu wpisanego w okrąg wiedząc że wysokość trapezu jest równa 4,jedna z jego
podstaw ma 6,a druga z nich jest średnicą tego okręgu.
2.Oblicz promień okręgu opisanego na trapezie równoramiennym o podstawach długości 5 i 13 oraz
wysokości 3.
3.Stosunek długości boków trójkąta jest równy 3:5:6.Oblicz sinus najmniejszego kąta w tym
trójkącie.
4.Dany jest trójkąt ABC, w którym AB=5 kąt BAC=45 stopni, ACB=30 stopni.Oblicz pole tego
trójkąta,wiedząc że cos15 stopni=√6+√2:4
5.Podstawa trapezu jest średnica opisanego na nim okręgu, a przekątne tego trapezu przecinają
się pod kątem 60stopni.Wykaż, że suma długości jego podstaw jest trzy razy większa od
promienia okręgu.
Dziękuje za pomoc.
12 paź 21:01
5-latek: Powiadasz na jutro ?
12 paź 21:05
olekturbo: Późno już

Pora do roboty. Co proponujesz?
12 paź 21:06
Marw: Tak na jutro, wiem że późno

co proponuję? Wziąć się do roboty...z waszą pomocą na pewno damy
radę.
Obliczyłem 1. wynik wyszedł 16+4
√5
2.R=
√62,5 Ale nie mam pojęcia czy są one dobre

12 paź 21:14
Marw: Coś ktoś

Jakieś pomysły do zadań 3,4,5.
12 paź 21:27
Eta:
1/ ok
12 paź 21:38
Eta:
2/ źle
12 paź 21:39
Marw: A z jakiego wzoru powinienem skorzystać w tym drugim zadaniu?
12 paź 21:45
Eta:
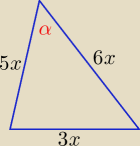
3/
Najmniejszy kąt leży naprzeciw najkrótszego boku i jest kątem ostrym
z tw. kosinusów
| | 25x2+36x2−9x2 | |
cosα= |
| = .... |
| | 2*5x*6x | |
sinα=
√1−cos2α=.....
12 paź 21:46
Janek191:
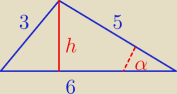
3) Niech a = 3 b = 5 c = 6
p = 0,5 (a + b +c) = 7
P =
√ p*(p−a)*(p − b)*( p − c) =
√ 7* 4* 2* 1 =
√56 = 2
√14
oraz
P = 0,5*6* h = 3 h = 2
√14
| | h | | 2 √14 | |
sin α = |
| = |
| ≈ 0,4988 |
| | 5 | | 15 | |
α ≈ 30
o
=======
12 paź 21:47
Eta:
@
Janek
Należało podać sinα ( a nie α

12 paź 21:48
Janek191:
Jest podany sinus α

12 paź 21:49
Marw: W 4 zadaniu zacząłem a:sin45=c:sin30 i a wyszło mi 5√2 i co dalej liczyć to nie wiem, bo
potem zacząłem liczyć c i głupoty po wychodziły
12 paź 21:55
Marw: c:sin30=b:sin105 i wyszło z tego b=10(√6+√2):4
12 paź 22:05
Marw: Zrobi ktoś te 4 i 2 zadanie?
12 paź 22:17
Eta:
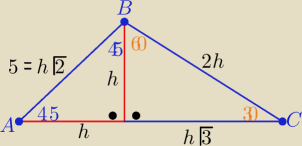
Mnie nie jest potrzebna ta informacja o cosinusie 15
o
Zadanie rozwiązuję tak:
| | 1 | | 1 | |
P= |
| *(h+h√3)*h= |
| h2(√3+1) |
| | 2 | | 2 | |
12 paź 22:28
Eta:
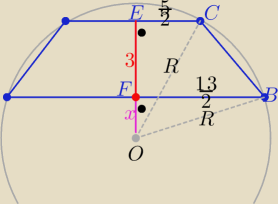
Dwa razy z Pitagorasa w trójkątach
OEC i OFB
| | 25 | | 169 | |
R2=(3+x)2+ |
| i R2=x2+ |
| |
| | 4 | | 4 | |
.................................
12 paź 22:34
Eta:
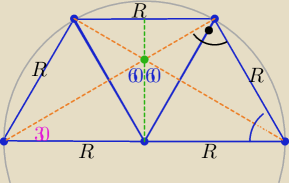
rys. powinien wystarczyć ( napisz odpowiedni komentarz
.............................
a=2R , b=R a+b=3R
12 paź 23:03
Eta:
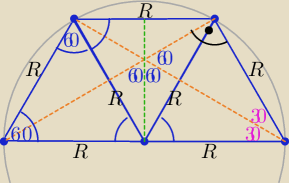
Na poprzednim rys. nie wiem czemu ale nie mogłam dokończyć oznaczeń miar kątów
(ginął mi cały rysunek ) ( jakieś duchy ,?

12 paź 23:13
Bogdan:
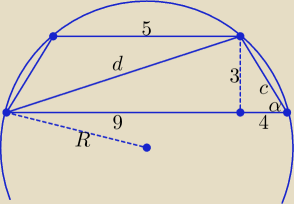
Proponuję skorzystać z twierdzenia sinusów w trójkącie o bokach: c, d, 13.
| | 3 | |
d = √81 + 9 = 3√10, c = √16 + 9 = 5, sinα = |
| |
| | 5 | |
| | 3√10 | | 5√10 | |
Z twierdzenia sinusów: |
| = 2R ⇒ R = |
| |
| | | | 2 | |
12 paź 23:42
Eta:


12 paź 23:49
Eta:
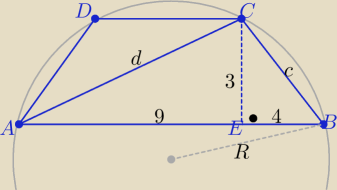
No to jeszcze
 3 sposób
3 sposób
zad.2 ( bez trygonometrii)
|AB|= a=13 , h= 3 , c=5 , d= 3p[10}
W trójkącie ABC
| | a*c*d | | 13*5*3√10 | | 5√10 | |
R= |
| i 4P(ABC)=2*39 to R= |
| = |
| |
| | 4P | | 2*39 | | 2 | |
13 paź 19:41
 Pora do roboty. Co proponujesz?
Pora do roboty. Co proponujesz?
 co proponuję? Wziąć się do roboty...z waszą pomocą na pewno damy
radę.
Obliczyłem 1. wynik wyszedł 16+4√5
2.R=√62,5 Ale nie mam pojęcia czy są one dobre
co proponuję? Wziąć się do roboty...z waszą pomocą na pewno damy
radę.
Obliczyłem 1. wynik wyszedł 16+4√5
2.R=√62,5 Ale nie mam pojęcia czy są one dobre 
 Jakieś pomysły do zadań 3,4,5.
Jakieś pomysły do zadań 3,4,5.
 3/
Najmniejszy kąt leży naprzeciw najkrótszego boku i jest kątem ostrym
z tw. kosinusów
3/
Najmniejszy kąt leży naprzeciw najkrótszego boku i jest kątem ostrym
z tw. kosinusów
 3) Niech a = 3 b = 5 c = 6
p = 0,5 (a + b +c) = 7
P = √ p*(p−a)*(p − b)*( p − c) = √ 7* 4* 2* 1 = √56 = 2√14
oraz
P = 0,5*6* h = 3 h = 2√14
3) Niech a = 3 b = 5 c = 6
p = 0,5 (a + b +c) = 7
P = √ p*(p−a)*(p − b)*( p − c) = √ 7* 4* 2* 1 = √56 = 2√14
oraz
P = 0,5*6* h = 3 h = 2√14


 Mnie nie jest potrzebna ta informacja o cosinusie 15o
Zadanie rozwiązuję tak:
Mnie nie jest potrzebna ta informacja o cosinusie 15o
Zadanie rozwiązuję tak:
 Dwa razy z Pitagorasa w trójkątach
OEC i OFB
Dwa razy z Pitagorasa w trójkątach
OEC i OFB
 rys. powinien wystarczyć ( napisz odpowiedni komentarz
.............................
a=2R , b=R a+b=3R
rys. powinien wystarczyć ( napisz odpowiedni komentarz
.............................
a=2R , b=R a+b=3R
 Na poprzednim rys. nie wiem czemu ale nie mogłam dokończyć oznaczeń miar kątów
(ginął mi cały rysunek ) ( jakieś duchy ,?
Na poprzednim rys. nie wiem czemu ale nie mogłam dokończyć oznaczeń miar kątów
(ginął mi cały rysunek ) ( jakieś duchy ,? 
 Proponuję skorzystać z twierdzenia sinusów w trójkącie o bokach: c, d, 13.
Proponuję skorzystać z twierdzenia sinusów w trójkącie o bokach: c, d, 13.


 No to jeszcze
No to jeszcze  3 sposób
zad.2 ( bez trygonometrii)
|AB|= a=13 , h= 3 , c=5 , d= 3p[10}
W trójkącie ABC
3 sposób
zad.2 ( bez trygonometrii)
|AB|= a=13 , h= 3 , c=5 , d= 3p[10}
W trójkącie ABC