Logarytmy Artix1500: Prosze o pomoc przy takim zadaniu z logarytmow

1		2
	+		< 1
5 − logx		logx − 1

Kacper: Podstaw logx=t.

J: i zrób odpowiednie założenia

Artix1500: No wlasnie robie ale pozniej wychodza mi takie cuda ze nie mam pojecia co z tym zrobic

Janek191:

1		2
	+		< 1
5 − t		t − 1

t − 1 + 2*(5 − t)
	< 1
( 5 − t)*( t − 1)

t − 1 + 10 − 2 t
	− 1 < 0
( 5 − t)*( t −1)

− t + 9		( 5 − t)*( t −1)
	−		< 0
( 5 − t)*( t − 1)		5 − t)*( t − 1)

− t + 9 + 5 t − 5 − t2 + t
	< 0
( 5 − t)*( t − 1)

− t2 + 5 t + 4
	< 0
( 5 − t)*( t − 1)

t2 − 5 t − 4
	> 0
( 5 − t)*( t − 1)

t2 − 5 t − 4
	< 0
( t − 5)*( t − 1)

itd.

Artix1500: No ok a co dalej bo nie wiem czy dobrze rozumuje a nie mam odpowiedzi

Artix1500: No mozna tak skrotowno napisac naprawde

J:

a
	< 0 ⇔ a*b < 0 ..... zastosuj
b

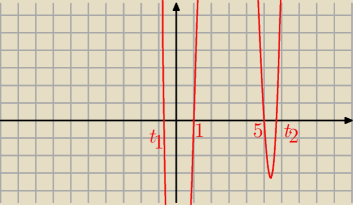
Janek191: Jak się nie pomyliłem, to : Δ = 25 − 4*1*(−4) = 25 + 16 = 41 √Δ = √41

	5 − √41
t1 =		= 2,5 − 0,5√41 ≈ − 0,7
	2

	5 + √41
t2 =		= 2,5 + 0,5√41 ≈ 5,7
	2

( t − 2,5 + 0,5 √41)*( t − 2,5 − 0,5√41)*( t − 5)*( t − 1) < 0 Mamy 2,5 − 0,5√41 < t < 1 lub 5 < t < 2,5 + 0,5√41 t = log x ; x > 0 2,5 − 0,5 √41 < log x < 1 lub 5 < log x < 2,5 + 0,5√41 10^{2,5 − 0,5√41} x < 10 lub 10⁵ < x < 10^{2,5 + 0,5 √41}

Kacper: Poprawna odpowiedź, to: x∊(0,10)∪(10⁵,+∞)

Kacper: Janek masz błędy przy odejmowaniu. 5 linijka 15:56

Janek191: Gdzie się pomyliłem ?

Artix1500: Ok dziekuje wszystkim za pomoc

Janek191: Faktycznie − znaki

Janek191: To Artix1500 sobie poprawi