Stereometria
katharina218: Suma pól powierzchni dwóch sześcianów jest równa 78, a suma ich objętości jest równa 35. Oblicz
długość krawędzi tych szecianów. Jak rozwiązać taki układ równań?
12 paź 11:50
J:
Mozna np. odgadnąć: a = 3 , b = 2
12 paź 11:54
Qulka:
6a2+6b2=78
a3+b3=35
12 paź 11:54
ICSP: albo próbować podstawieniami u = a + b oraz v = ab oczywiscie, u,v > 0
12 paź 11:55
katharina218: J: Odgadnąć to ja sobie odgadłam

Qulka : Taki układ właśnie nie wiem jak rozwiązać. Bo ani podstawianie mnie nie ratuje, ani
przeciwne współczynniki

ICSP: mogę sobie podstawić tylko jak korzystam z wzorów skróconego mnożenia to mam a
2b i ab
2
więc takie podstawienia nic mi nie dają ...
12 paź 15:14
ZKS:
Pokaż jak liczysz.
12 paź 15:30
katharina218: Ze wzorów skróconego mnożenia mam
a
2+b
2 = (a+b)
2−2ab=13
a
3+b
3 = (a+b)
3−3a
2b−3ab
2=35
Teraz nawet jeśli za a+b podstawie sobie x a za ab=y to i tak w sumie sześcianów będę mieć 3ya
i 3yb. Po wyciągnięciu przed nawias otrzymuję układ:
x
2 − 2y =13
x
3 − 3yx = 35
...

12 paź 15:48
ZKS:
To taki problem z pierwszego równania wyznaczyć y i wstawić do drugiego?
12 paź 16:09
katharina218: Tak, bo potem otrzymuję wielomian i żeby go rozwiązać muszę skorzystać z tw.Bezout, a tego nie
ma na matmie podstawowej (tylko na rozszerzeniu). Więc chodzi mi o rozwiązanie podstawowymi
zależnościami (pomijam fakt że suma sześcianów też test na rozszerzeniu). Więc proszę ZKS
napisz mi rozwiązanie tego układu korzystając z wzorów obowiązujących na matematyce
podstawowej.
12 paź 16:16
ZKS:
Nie rozumiem, a to na podstawie zabraniają używać zagadnień z rozszerzenia?
12 paź 16:28
katharina218: Nie, nie zabraniają, ale ich nie uczą. Nie ma tego w programie. Zwykły uczeń nie ma pojęcia o
istnieniu czegoś takiego, a musi rozwiązać zadanie innym sposobem. Dlatego pytam Cię JAKIM?
Chyba też masz z tym problem skoro nie potrafisz mi podać rozwiązania sposobem podstawowym

12 paź 16:32
Qulka:
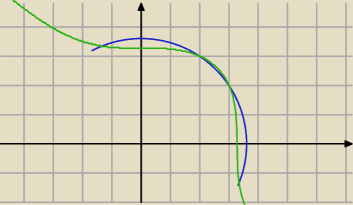
metodą podstawową ..jak widać na obrazku w 1 ćwiartce (bo to krawędzie więc dodatnie) jest
tylko rozwiązanie z=3 b=2 lub a=2 b=3
13 paź 13:33
Qulka: albo metodą z podstawówki którą zaproponował
J zgadywać suma kwadratów jakich liczb daje
13

i sprawdzać ich sześciany
13 paź 13:35
daras: to w podstawówce uczą się na pamięć
3 
13 paź 14:57
 Qulka : Taki układ właśnie nie wiem jak rozwiązać. Bo ani podstawianie mnie nie ratuje, ani
przeciwne współczynniki
Qulka : Taki układ właśnie nie wiem jak rozwiązać. Bo ani podstawianie mnie nie ratuje, ani
przeciwne współczynniki ICSP: mogę sobie podstawić tylko jak korzystam z wzorów skróconego mnożenia to mam a2b i ab2
więc takie podstawienia nic mi nie dają ...
ICSP: mogę sobie podstawić tylko jak korzystam z wzorów skróconego mnożenia to mam a2b i ab2
więc takie podstawienia nic mi nie dają ...


 metodą podstawową ..jak widać na obrazku w 1 ćwiartce (bo to krawędzie więc dodatnie) jest
tylko rozwiązanie z=3 b=2 lub a=2 b=3
metodą podstawową ..jak widać na obrazku w 1 ćwiartce (bo to krawędzie więc dodatnie) jest
tylko rozwiązanie z=3 b=2 lub a=2 b=3
 i sprawdzać ich sześciany
i sprawdzać ich sześciany
