największa wartość funkcji ana: Pewne ciało porusza się ruchem prostoliniowym zgodnie ze wzorem s(t)=6t²−0,5t³, gdzie s(t) oznacza drogę mierzoną w metrach, natomiast t czas mierzony w sekundach. W którym momencie t∊<0,12> prędkość ciała jest największa? Oblicz tę prędkość. ja liczyłam od tego pochodną, następnie warunek konieczny i warunek wystarczający a potem wartości funkcji na końcach przedziałów, ale niestety nie chce mi wyjść odpowiedź zgodna z kluczem

J: t = 8 sekunda

Janek191: v(t) = s '(t) = 12 t −1,5 t² = t*( 12 − 1,5 t) t₁ = 0 t₂ = 8

	t1 + t2
t =		= 4
	2

dadam: v(t)=12t−1,5t²=−1,5t*(t−8) t=0 ∨ t=8

	0+8
tmax=		=4
	2

J: @Janek191 ... w czwartej sekundzie pochodna osiaga maksimum, a nie ciało :

Janek191: @J : Podaj obliczenia.

J: Obliczenia czego ?

J: dobra .... nie było tematu ...mój błąd

Janek191: Czasu .

ana: a czemu to nie chce wyjść moim sposobem?

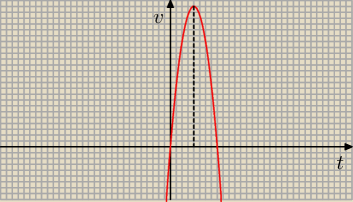
dadam: We wzorze na prędkość masz parabole (ekstremum w wierzchołku − stąd średnia arytmetyczna z miejsc zerowych) Ale można też tak: v')t)=12−3t=−3(t−4) t=4

dadam: mamasz policzyć max prędkości więc jak chcesz pochodnymi liczyć to musisz policzyć pochodną prędkości

J: Zapewne tak jak ja, liczysz maksimum s(t) , a nie v(t)

daras: Liczysz maksimum v(t) = 12t −1,5t² czyli v' =a(t) = 12 −3t = 0 stąd t = 4 s wtedy ciało przestaje przyspieszać więc prędkość ma maksymalną