Rozwiąż nierówność kero: mam problem z kilkoma zadaniami. 1). −x³+x²+x−1 ≥0 i ja rozwiązuje to w taki sposób. −x²(x−1)+1(x−1)≥0 /*(−1) x²(x−1)−1(x−1)≤0 (x²−1)(x−1)≤0 (x+1)(x−1)(x−1)≤0 x=1 v x=−1 v x=−1 nie wiem gdzie robię błąd ponieważ wychodzi mi że xε<−1 1> 2). x⁴−5x³+4>0 x²=t t²−5t+4>0 Δ=9 t1=4 t2=1 x=√t (x−2)(x−1)>0 xε(1 2) tu również nie mam pomysłu gdzie robię błąd 3). x³+6x²+11x+6>0 a tego kompletnie nie wiem jak ugryźć.

Janek191: x³ + 6 x² + 11 x + 6 > 0 x = − 1, bo − 1 + 6 − 11 + 6 = 0 Dzielimy przez x + 1 ( x³ + 6 x² + 11 x + 6) : ( x + 1) = x² + 5 x + 6 −x³ − x² −−−−−−−−−− 5 x² + 11 x − 5 x² − 5 x −−−−−−−−−−−−−− 6 x +6 − 6 x − 6 −−−−−−−−−− 0 x² + 5 x + 6 = ( x + 3)*(x + 2) Mamy zatem ( x + 3)*( x + 2)*( x + 1) > 0 Dokończ

kero: dziękuje

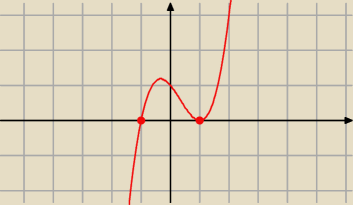
Janek191: 1) − x³ + x² + x −1 ≥ 0 − x²*( x − 1) + 1*( x −1) ≥ 0 ( x − 1)*( − x² + 1) ≥ 0 (x −1)*( 1 − x²) ≥ 0 ( x − 1)*( 1 − x)*( 1 + x) ≥ 0 / *( −1) ( x − 1)*( x − 1)*( x + 1) ≤ 0 Dokończ: )

kero: 1) xε<−∞ −1> v <1> 3) xε(−3 −2) v (−1 +∞)

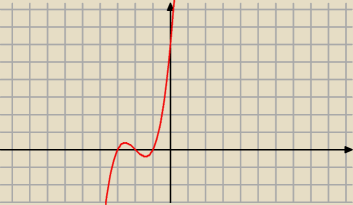
Janek191: Ok. z.3 x ∊ ( − 3 ; − 2) ∪ ( − 1; +∞ )

kero: Udało mi się zrobić drugie zadanie zostawię rozwiązanie dla innych. x⁴−5x²+4>0 X⁴−4x²−x²+4>0 x²(x²−4)−1(x²−4)>0 (x²−1)(x²−4)>0 (x−1)(x+1)(x−2)(x+2)>0