funkcja logarytmiczna dziedzina Heronek: Dziedzina f. log. Męczę się z tym zadaniem już dłuższy czas, pomocy: Wyznacz dziedzinę funkcji:

	x
f(x) = log1/2		(cały logarytm jest pod pierwiastekiem, nie pisze go bo wygląda to
	x2−1

	x
wtedy tak: √log1/2		)
	x2−1

Janek191:

	x
log0,5		≥ 0
	x2 − 1

x
	> 0
x2 − 1

Janek191:

	x		x
czyli log0,5		≥ log0,5 1 ⇒		≤ 1
	x2 − 1		x2 − 1

	x
i		> 0
	x2 − 1

Heronek: z tego pierwszego wychodzi mi coś takiego później?: (−x² + x + 1)(x² − 1) ≤ 0

	1−√5		1+√5
z lewej części wychodzi mi że x∊(		,		) a z prawego x ∊ (−1,1) czy to
	2		2

jest wogóle dobrze? Jaki znak powinien być między tymi dwoma koniunkcja czy alternatywa? I czy pomiędzi warunkiem 1 założeń a warunkiem drugim powinna być koniunkcja?

Heronek: a ten drugi warunek: czy wyjdzie on tak czy dobrze mi się wydaje że gdzieś mam błąd: x(x²−1) > 0 x>0 |x|>1 x>1 v x<−1 x∊(0, +∞)

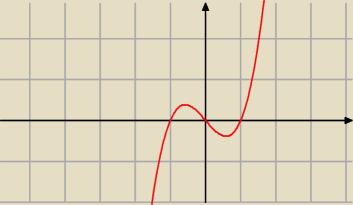
Janek191: Odczytaj z wykresu :

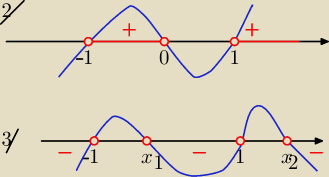
Eta: 1/ x²−1≠0 ⇒ x≠1 , x≠ −1

	x
2/		>0 ⇒ x(x−1)(x+1)>0 ⇒ x∊(−1,0)U (1,∞)
	x2−1

	x
3/		≤1 ⇒ (x−1)(x+1)(−x2+x+1)≤0
	x2−1

	1−√5		1+√5
miejsca zerowe f: −x2+x+1 x1=		v x2=
	2		2

	1−√5		1+√5
x∊(−∞, −1)U(		, 1) U(		, ∞)
	2		2

teraz wybierz część wspólną tych trzech warunków

	1−√5		1+√5
otrzymasz : Df= (		,0) U (		, ∞)
	2		2

Eta: Popraw Na 3/ rys w miejscach x₁ i x₂ mają być przedziały domknięte ! (nie zauważyłam nierówności słabej ≤ 0

Heronek: Dziękuję bardzoooo! Teraz wszystko rozumiem i kilka podobnych przykładów wyszło mi super szybko. Dziękuję. Uwielbiam to jak w twoich odpowiedziach wszystko jest przejrzyste i od razu zrozumiałe

Eta: