Rozwiąż równainie Wafel: rozwiąż równanie

	π		√2
sin(2x+		) = −
	4		2

	π		√2
rozwiązywalam to tak, że podstawiałam, z= 2x+		, nastepnie sinz=−
	4		2

tylko nie wiem jak obliczyc z.

Tadeusz: odczytać z wykresu

Wafel: ok, mam z= 5/4π lub −π/4 ale problem w tym ze gdy podstawiam do wyrazenia w nawiasie to wychodzą złe znaki

Janek191:

	π		√2
sin ( 2 x +		) = −
	4		2

	π		π		π		π
2 x +		= −		+ 2π*k lub 2 x +		= 2π +		+ 2π*k
	4		4		4		4

Janek191:

	π		π
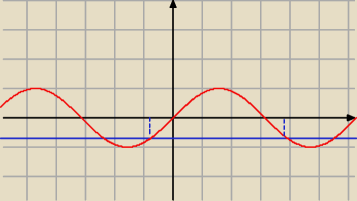
Po lub powinno być 2 x +		= π +		+ 2π*k − rysunek
	4		4

Wafel:

	π
Janek, z wyrazenia "po lub" wychodzi x =		+ kπ
	2

	π
mój problem polega na tym, że w odpowiedziach ze zbioru jest −
	2

No chyba że ja nadal coś źle licze?

Janek191: Nie

	π
x =		+ π*k
	2

Janek191: To jest to samo − dla k = − 1

Wafel:

	π
w odp mam −		+ kπ
	2

Mila: W drugim zapomniałam dopisać (+π) Masz obliczyc x.

	π		√2
sin(2x+		)=−
	4		2

	π		π		π		3π
2x+		=		+π+2kπ lub 2x+		=		+π+2kπ
	4		4		4		4

	3π
2x=π+2kπ lub 2x=		+2kπ /:2
	2

	π		3π
x=		+kπ lub x=		+kπ
	2		4

spr.

	π		π		π		π		√2
L=sin(2*		+		)=sin(π+		)=−sin(		)=−		=P
	2		4		4		4		2

3π

π

3π

π

7π

π

L=sin(2*

+

)=sin (

+

)=sin(

)=sin(2π−

)=

4

4

2

4

4

4

	π		√2
=−sin(		)=−
	4		2

Mila: Wafel, można różnie napisać serię rozwiązań dla równania

	√2
sinx=−
	2

1)Ja ustalam serię rozwiązań w przedziale <0,2π>

	π		π		3π		√2
sin		=U{√2{2} lub sin(π−		)=U{√2{2} (⇔sin		=
	4		4		4		2

2) teraz dla ujemnych wartości tak:

	√2
sinx=−
	2

	π		3π
x=		+π+2kπ lub x=		+π+2kπ
	4		4

	5π		7π
x=		lub x=		+2kπ
	4		4

Można też tak:

	√2
sinx=−
	2

	π		3π
x=−		+2kπ lub x=−		+2kπ
	4		4

jeśli podstawisz k=1 to otrzymasz :

	π		7π		3π		5π
x=−		+2π=		lub x=−		+2π=
	4		4		4		4

W obu przypadkach musisz wiedzieć jakie jest rozwiązanie równania

	√2
sinx=
	2