Zadanko
Edyta : Proszę o pomoc
11 paź 17:17
PW : Tam na pewno jest jedna druga?
11 paź 17:22
Edyta : Nie,
Przepraszam za pomyłkę

11 paź 17:26
Edyta : Pomoże ktoś ?

11 paź 18:06
sushi_gg6397228:
zacznij od
z= x+iy
11 paź 18:10
11 paź 18:21
Edyta : dobrze ?
11 paź 18:21
sushi_gg6397228:
liczymy
| 1 | |
| =.... usuwamy "i" z mianownika mnożąc przez sprzężenie |
| z | |
11 paź 18:23
sushi_gg6397228:
śpisz tam ?
11 paź 18:36
Edyta : Umiem robić tylko sprzężenie jak są pierwiastki. Z liczb zespolonych dopiero miałam 1 lekcje

11 paź 18:40
sushi_gg6397228:
tu działa tak samo np:
| 4 | | 1−i | | 4(1−i) | |
| * |
| = |
| = 2 − 2i i Re(...)= 2 Im(...)= −2 |
| 1+i | | 1−i | | 2 | |
11 paź 18:46
Edyta : | 1 | | x−iy | | 1(x−iy) | | 1 | |
| * |
| = |
| = |
| |
| x+iy | | x−iy | | (x−iy)2 | | x−iy | |
11 paź 19:24
sushi_gg6397228:
mianownik źle
x2 − (iy)2= ....
11 paź 19:25
Edyta : aaaa, ok
dzięki
11 paź 19:27
sushi_gg6397228:
licz i zapisuj ile wyszło
11 paź 19:27
11 paź 19:42
sushi_gg6397228:
| a+b | | a | | b | |
| = |
| + |
| rozbijamy na dwa ułamki |
| c+d | | c+d | | c+d | |
11 paź 19:46
11 paź 19:51
sushi_gg6397228:
to Re (
1z) = ....
11 paź 19:52
Edyta : ?
nie rozumiem tego zadania
11 paź 19:56
sushi_gg6397228:
bingo
11 paź 19:57
sushi_gg6397228:
to jest tak samo jakby było z pierwiastkami
| √3 | |
| i wynik zapisz w postaci a+ b√3, gdzie a,b ∊ W |
| 2−√3 | |
11 paź 19:58
Edyta : | | 1 | |
czyli te Re |
| jest dobrze   |
| | z | |
11 paź 20:00
sushi_gg6397228:
tak
11 paź 20:02
Edyta : | | 1 | |
a ta nierówność Re( |
| ) > Im ? |
| | z | |
to wszytko ?
11 paź 20:02
Edyta : Odp.: a+bx , gdzie a,b ∊ W
?
11 paź 20:04
sushi_gg6397228:
teraz musisz policzyć prawą stronę
i*z= ...
11 paź 20:06
Edyta : iz = i(x+iy) = ix + i2y
11 paź 20:08
sushi_gg6397228:
i2=...
11 paź 20:10
Edyta : Im (iz) = x+y ?
11 paź 20:10
Edyta : −1
11 paź 20:11
Edyta : czyli
Im(iz) = x ?
11 paź 20:12
sushi_gg6397228:
iz= −y + ix
Im(iz)= x
więc zapisz co wyszło do nierówności
11 paź 20:13
11 paź 20:15
sushi_gg6397228:
i teraz dopiero są schody; tamto bylo pikus
11 paź 20:15
Edyta : :(
11 paź 20:16
sushi_gg6397228:
założenia x, y ≠ 0
na jedna strone, wspolny mianownik
11 paź 20:17
11 paź 20:19
sushi_gg6397228:
a gdzie jakiś dodatek do "x" w drugim ułamku ?
11 paź 20:20
Edyta : x2
11 paź 20:33
sushi_gg6397228:
wspolny kreska a potem "x" przed nawias i włączamy myślenie
11 paź 20:35
11 paź 20:53
sushi_gg6397228:
| x [1−(x2+y2)] | |
| >0 mianownik zawsze dodatni przy naszych założeniach |
| x2+y2 | |
więc
x [1−(x
2+y
2)] > 0
liczymy "miejsca zerowe"
x=0 lub 1− (x
2+y
2)= 0
x=0 lub x
2+y
2=1 −−> a to nic innego jak równanie okręgu o środku (0;0) i promieniu 1
11 paź 20:57
sushi_gg6397228:
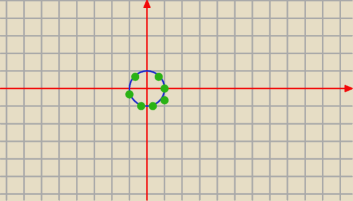
11 paź 21:00
Edyta : Wielkie dziękuje

11 paź 21:03
sushi_gg6397228:
trzeba jeszcze dać odp. do nierówności
11 paź 21:06
sushi_gg6397228:
i rozpatrzeć przypadki
masz 4 pola wewnatrz okregu oraz 4 na zewnatrz
11 paź 21:07
Edyta : ...
11 paź 21:13
sushi_gg6397228:
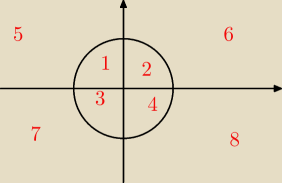
i sprawdzamy jaki bedzie znak w kazdym polu z cyfrą
x [1− (x
2+y
2)] >0
dla pól 1; 2; 3; 4
x2+y2 <1
dla pol 5 ;6 ; 7; 8;
x2+y2 >1
wysil się trochę
11 paź 21:17







 i sprawdzamy jaki bedzie znak w kazdym polu z cyfrą
x [1− (x2+y2)] >0
dla pól 1; 2; 3; 4 x2+y2 <1
dla pol 5 ;6 ; 7; 8; x2+y2 >1
wysil się trochę
i sprawdzamy jaki bedzie znak w kazdym polu z cyfrą
x [1− (x2+y2)] >0
dla pól 1; 2; 3; 4 x2+y2 <1
dla pol 5 ;6 ; 7; 8; x2+y2 >1
wysil się trochę