rozwiąż nierówność ola: |x²+3|=|x²+2x+5|+|x−5| mógłby mi ktoś pomóc

ICSP: Pierwsze dwie wartości bezwzględne możesz skasować.

Eta: "skasować" ? należy bilet tramwajowy

ola: Ale jak mozesz to rozwiazac bo ja dopiero sie tego uczę

ICSP:

ola: Ok zrobiłam a taki przykład |x²−|x||<2

[P[misiek]]: x²+3>0 niezależnie od m x²+2x+5=(x+1)²+4 >0 niezależnie od m mamy więc równanie: x²+3=x²+2x+5+|x−5|

ICSP: x² + 3 = x² + 2x + 5 + |x − 5| |x − 5| = −2x −2 i teraz rozwiązuj w przedziałach : 1^o x ∊ (− ∞ ; 5] 2^o x ∊ (5 ; + ∞)

PW : |x − 5| = − 2(x+1), dla x > −1 nie ma co rozwiązywać, bo i tak rozwiązań nie ma (prawa strona jest ujemna) , ograniczymy się więc tylko do x ≤ −1.

ola: Ok a moglibyscie mi pomóc w tym |x²−|x||<2

pigor: ..., ... ... ⇔ |x−5|= −2x−2 i −2x−2 ≥ 0 ⇔ (x−5= −2x−2 v x−5= 2x+2) i x ≤ −1 ⇔ ⇔ (3x= 3 v x= −7) i x ≤ −1 ⇔ (x=1 i x ≤ −1) v (x= −7 i x ≤ −1) ⇔ ⇔ ∅ v x= −7 ⇔ x= −7. ...

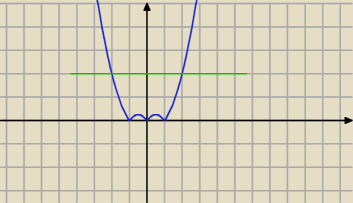
qulka: x∊(−2;2)

pigor: ..., oj, tego analitycznie .nie przepuszczę, a więc patrz, myśl i ...... ucz się, bo w dużej większości N−lki(le) raczej tak nie uczą, a nie pożałujesz, a więc : |x²−|x|| < 2 ⇔ −2 < x²−|x| < 2 ⇔ |x|²−|x|+2 > 0 i |x|²−|x|−2 < 0 ⇔ ⇔ (|x|∊R, bo a=1 i Δ= −7<0) i (|x|+1)(|x|−2) < 0 ⇔ ⇔ x∊R i −1 < |x| < 2 ⇔ −1 < |x| < 2 ⇔ |x| >−1 i |x| < 2 ⇔ ⇔ x∊R i −2< x< 2 ⇔ x∊[−2;2] . ...