analityczna Bogusia: Cześć Oblicz długość najdłuższego boku trójkąta , którego boki zawarte są odpowiednio w prostych l i k oraz w osi y l: y=x+4 , k: y=−x−3 prosze o pomoc

Michał: dł = 7

Bogusia: za wiele mi to nie daje jak to rozwiązałeś?

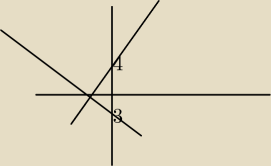
Michał: fg

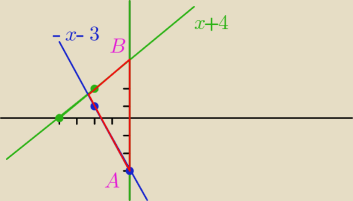
Godzio: AB = ? szukamy punktu wspólnego dla y=−x−3 i x=0 x=0 y=−x−3 czyli y=−3 A(0,−3) teraz prostej y=x+4 i x=0 x=0 y=x+4 czyli y=4 => B(0,4) |AB| = √ (0+0)² + (4−(−3))² = √49 = 7

Michał: Na oko rysowane. tam jest oczywiście −3 arysunek przedstawia układ współrzędnych. Prosta y jest przeciwprostokątną i jest najdłuższym bokiem.

Michał: Na oko rysowane. tam jest oczywiście −3 arysunek przedstawia układ współrzędnych. Prosta y jest przeciwprostokątną i jest najdłuższym bokiem.

Michał: Na oko rysowane. tam jest oczywiście −3 arysunek przedstawia układ współrzędnych. Prosta y jest przeciwprostokątną i jest najdłuższym bokiem.

Michał: Na oko rysowane. tam jest oczywiście −3 arysunek przedstawia układ współrzędnych. Prosta y jest przeciwprostokątną i jest najdłuższym bokiem. Obliczona jest z różnicy 4 − (−3)

Bogusia: dzięki Godzio i Michał

Michał: Łatwo podać rozwiązanie. Zwróć uwagę że podane proste mają współczynnik kierunkowy równy 1 i −1. A więc są to elementarne proste y=x jedynie z przesunięciami i zmianą monotoniczności. A więc łatwo sobie je wyobrazić ' w głowie'. Pozostaje tylko określić która prosta jest najdłuższa. A dalej to już zwykłe odejmowanie