| −4 | 3 | |||
Jeżeli wykres f(x)= | + | przesuniemy o wektor | ||
| x−p | 5 |
| 1 | 1 | 2 | 2 | |||||
v=[2 | b+4 | ; | b+ | ] to powstanie hiperbola o środku symetrii w początku | ||||
| 2 | 2 | 3 | 5 |
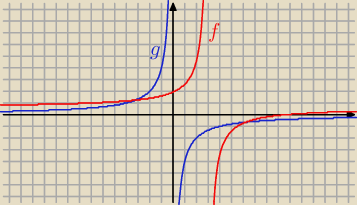
| − 4 | 3 | 2 | 2 | |||||
g(x) = | + | + | b + | |||||
| x − 52b −92 − p | 5 | 3 | 5 |
| 5 | 9 | |||
− | b − | − p = 0 | ||
| 2 | 2 |
| 3 | 2 | 2 | 2 | 3 | |||||
+ | b + | = 0 ⇒ | b = − 1 ⇒ b = − | ||||||
| 5 | 3 | 5 | 3 | 2 |
| 5 | 3 | 9 | ||||
− | *( − | ) − | = p | |||
| 2 | 2 | 2 |
| − 4 | 3 | − 20 + 3*( x −3) | ||||
f(x) = | + | = | = 0 ⇔ 3 x = 29 | |||
| x − 3 | 5 | 5*(x −3) |