nierówność z parametrem
truskawka: Dla jakich wartości parametru m (m∊R) zbiór rozwiązań nierówności
x
2+(m−1)x+m
2≤0
| | x−1 | |
zawiera się w zbiorze rozwiązań nierówności |
| <0? |
| | x+1 | |
(x−1)(x+1)<0
x∊(−1;1)
x
2+(m−1)x+m
2≤0
Δ=(m−1)
2−4m
2−(m−1−2m)(m−1+2m)=−3(m+1)(m−
13)
m∊(−
∞,−1>u<
13,+
∞)
I...nie wiem, co dalej
10 paź 18:55
J:
1) Δ ≥ 0
2) xw ∊ (−1,1)
3) f(−1) > 0
4 f(1) > 0
10 paź 18:59
:): (x−1)(x+1)=x
2−1
żeby oba miały te same pierwiastki to x
2+(m−1)x+m
2=x
2−1
a z tego (m−1)=0, m
2=−1 wiec tak sie nie da
10 paź 18:59
J:
Zadanie sprowadza się do: dla jakiego m pierwiastki równania ......
należą do przedziału (−1,1)
10 paź 19:06
truskawka: @J: dlaczego f(−1) >0 i f(1) >0?
@
:: musi się dać xD
10 paź 19:07
:): aaaa ZAWIERA SIĘ..ok..bo przeczytałem POkrywa sie
10 paź 19:07
:): f(−1)>0 jest po to, żeby pierwiastek pojawił sie przed −1...anagloczinie f(1)
10 paź 19:09
J:
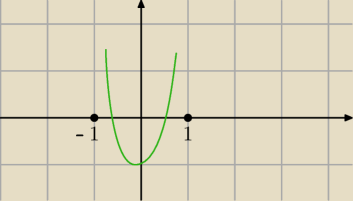
teraz widzisz ?
10 paź 19:10
truskawka: hmm ok czyli:
f(1)>0
1+m2>0
m2>−1
m∊R
f(−1)>0
1−m+1+m2>0
m2−m+2>0
Δ=1−8<0
a>0
m∊R
coś takiego?
10 paź 19:17
truskawka: ?
10 paź 19:37
truskawka: co dalej z tym zrobić?
10 paź 22:11
truskawka: ktoś coś?
10 paź 22:39
sushi_gg6397228:
dzisiaj nie mam już ochoty na kolejne owoce
10 paź 22:40
truskawka: no nie, jak tak można.....?
spróbuj pomyśleć
10 paź 22:45
sushi_gg6397228:
obaliłem 6 gruszek i 1 jabłko
a gdzie reszta punktów policzona
10 paź 22:46
truskawka: No, czyli ani jednej truskawki dzisiaj
Policzyłam Δ tylko nie wiem, czemu ma być ≥ 0 skoro w nierówności jest ≤
10 paź 22:50
sushi_gg6397228:
bo w zadaniu podali, że rozwiązania mają zawierać sie w przedziale (−1; 1) a to oznacza, że
parabola musi mieć miejsca zerowe patrz rysunek 19.10)
f(1) do bani
f(−1) dobrze policzony
10 paź 22:56
truskawka: No tak, podstawiłam za "m" xD
więc:
f(1)=1+m−1+m
2<0
m
2+m<0
m(m+1)<0
m∊(−1;0)
a skoro Δ>0 to przedział będzie m∊(−1;
13)
ale w takim razie odpowiedzią byłby przedział (−1;0) a to się nie zgadza
10 paź 23:03
sushi_gg6397228:
f(1) >0
10 paź 23:06
truskawka: no tak, m∊(−∞;−1) u(0;+∞)
no i z Δ wyszło m∊(−1;13)
czyli by wychodziło, że m∊(0;13) a w odpowiedziach jest m∊(−∞;−1) u(0;+∞)
11 paź 09:42
sushi_gg6397228:
to podstaw
m= −9 i zobacz co da nierówność
11 paź 11:09
truskawka: dla m=−9:
x2−10x+81≤0
Δ=100−4*81<0
Czyli brak rozwiązań. W takim razie w odpowiedziach jest błąd?
11 paź 11:28
sushi_gg6397228:
a może przykład był z nierównością w drugą stronę ?
policz jeszcze końce przy delcie
11 paź 11:33
Kacper:
Zbiór pusty zawiera się w zbiorze (−1,1).
Nie ma żadnego błędu w odpowiedzi, jeśli jest to dodane do rozwiązania.
11 paź 12:05