PW : Tradycyjny komentarz "mową polską".
Jest to typowe doświadczenie dwuetapowe: najpierw wybieramy losowo jedną z urn, potem z tej urn
y wybieramy jedną z kul. W szkolnej praktyce panuje tendencja do rozwiązywania takich zadań w
sposób pokazany przez
Milę.
Ponieważ widziałem, że chciałeś zbudować przestrzeń zdarzeń elementarnych (chwalebne, tak
powinno się robić), wytłumaczę jak wygląda taka przestrzeń.
Zdarzeniami elementarnymi są
pary
(urna, kula z tej urny).
Zdarzeń elementarnych nie jest znowu tak dużo jak liczyłeś. Jeżeli urny oznaczyć symbolami A i
B tak jak to zrobiłeś, a kule białe i czarne symbolami b
A. b
B i c
A, c
B, to zdarzenia
elementarne są raptem 4:
Ω = {(A,b
A), (A, c
A), (B, b
B), (B, c
B)}.
Nie działa jednak klasyczna definicja prawdopodobieństwa. Nie można przyjąć, że wszystkie
zdarzenia są jednakowo prawdopodobne, chociażby z tego względu, że częściej wylosujemy urnę AB
niż A. Prawdopodobieństwa losowania kul też są różne.
Z tego względu przyjęło się (jest odpowiednie twierdzenie, które mówi, że tak będzie rozsądnie
i poprawnie teoretycznie) w takich przestrzeniach definiować prawdopodobieństwo na zasadzie
mnożenia:
(*) P(x, y) = P
1(x)·P
2(y),
gdzie P
1(x) oznacza prawdopodobieństwo zdarzenia x w przestrzeni Ω
1 (takiej jaka jest
poprawna tylko dla doświadczenia opisanego przez pierwszy element pary), w tym wypadku P
1(A)
| | 4 | | 16 | |
= |
| i P(B) = |
| , natomiast P2(y) oznacza prawdopodobieństwo zdarzenia y w |
| | 20 | | 20 | |
przestrzeni Ω
2 (stanowiącej model drugiego doświadczenia), w tym wypadku są to
prawdopodobieństwa losowania kul w poszczególnych typach urn.
Wszystko to "streszcza się w postaci takiego właśnie drzewka, żeby uczeń mógł w ogóle to
zadanie rozwiązać, gdyż opis teoretyczny jest skomplikowany. Trochę inaczej można zbudować
model, gdy zna się twierdzeie o prawdoopodobieństwie całkowitym, ale jeszcze go pewnie nie
znasz.
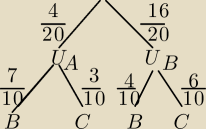Na drzewku masz przebieg doświadczenia losowego.
4UA
7B,3C
16UB
4B,6C
A− wylosowano białą kulę
