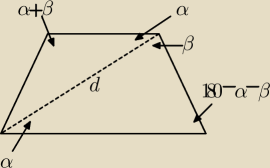
Oblicz w trapezie równoramiennym długości podstaw. nacix: Oblicz w trapezie równoramiennym długości podstaw.

	dsinβ
Jedna odpowiedź jest taka: a=		i wiem czemu tak jest.
	sin(α+β)

	dsin(2α+β)
Ale nie wiem czemu: b=
	sin(α+β)

nacix: proszę o pomoc

daras: skoro jest równoramienny, to odejmij od dłuższej krótszą i 2x( Δ prostokątny)

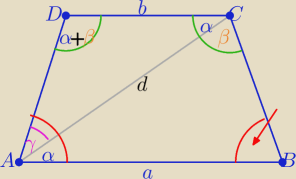Eta: |<B|=180^o−(α+β) to γ+α=<B ⇒ |<γ|= 180^o−(2α+β) sin[180^o−(α+β)]= sin(α+β) i sinγ= sn[180^o−(2α+β)]= sin(2α+β) z tw. sinusów w trójkątach ABC i ADC

d		b		d		a
	=				=
sin(α+β)		sinγ		sinB		sinβ

	dsin(2α+β		dsinβ
b=		i a=
	sin(α+β)		sin(α+β)

nacix: Dziękuje bardzo, niby takie banalne, a nie mogłam tego zauważyć