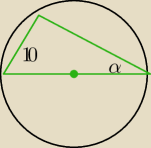
Pomocy Karolina: Proszę o w miarę jasne rozwiązanie Przyprostokątna trójkąta prostokątnego ma długość 10. Miara kąta ostrego leżącego naprzeciw tej przyprostokątnej wynosi 30. Oblicz długość okręgu opisanego na tym trójkącie

J: O = 2πR , gdzie R jest połową przeciwprostokątnej trójkąta: R = 10

J:

10		10		1
	= sin30 ⇔⇔		=		⇔ 2R = 20 ⇔ R = 10
2R		2R		2

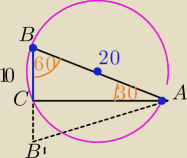
Mila: ΔBB'C− Δrównoboczny o boku 20.

	1
R=		|AB|=10
	2

J: Korzystamy z własności: przeciwprostokątna trójkąta prostokątnego jest średnicą okręgu opisanego na tym trójkącie

J: Ta własność z kolei wynika z twierdzenia,że kąt wpisany w okrąg jest połową kąta środkowego, opartego na tym samym łuku

Karolina: Dlaczego?

J: Popatrz na rysunek... kąt środkowy = 180⁰ , zatem kąt wpisany = 90⁰ (kąt prosty)