zespolone Benny: Czy geometryczna interpretacja |z+i|=|z−i| będzie po prostu oś rzeczywista?

J: Zbiór pusty: Iz + iI = Iz − iI ⇔ z + i = z − i ⇔ z − z = 2i ⇔ 0 = 2i ....sprzeczność

Benny: To nie ma wyglądać tak? √x²+(y+1)²=√x²+(y−1)² ⇔ (y+1)²=(y−1)² ⇒ y=0 i x∊R

J: mogę się mylić...

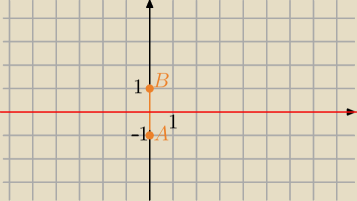
Mila: |z+i|=|z−i| to symetralna odcinka AB, gdzie: A=(0,−1) B=(0,1) y=0

Benny: Czyli jest tak jak napisałem wyżej? Innym sposobem niż podałem da się to rozwiązać?

J: a jednak się myliłem

Mila: Dobrze rozwiązałeś. {z: |z−a|=|z−b|}− symetralna odcinka ab |z−1|=|1+5i−z| symetralna (1,0)(1,5) piszesz zwyczajnie symetralną albo przekształcasz tak, jak to zrobiłeś.

Benny: Z tą symetralną mi się podoba, dziękuje . Może na zajęciach ktoś wspomni o tym. Zaraz pewnie się tu znowu odezwę z innym przykładem.

Benny: Co z takim przykładem? {z∊ℂ: |z+i|+|z−i|=3} trochę słabo mi się widzi robić tak jak wyżej. Gdzieś wyczytałem, że ma to być elipsa, ale my na zajęciach nie mieliśmy nic o równaniu elipsy

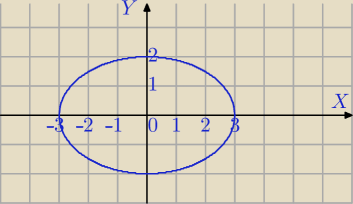
Mila: Równanie elipsy:

x2		y2
	+		=1 środek w (0,0),
a2		b2

Przykład :

x2		y2
	+		=1
32		22

Przekształcaj , a zobaczymy co wyjdzie.

henrys: z definicji elipsy:miejsce geometryczne punktu, którego suma odległości od dwóch ustalonych punków (ognisk) jest stała. Ogniskami są tutaj punkty (0,i) i (0,−i) suma odległości r₁+r₂=3

Mila: Jest jeszcze inny sposób, ale muszę sobie przypomnieć.

Benny:

	4		4
Wyszło mi		x2+		y2=1, wklepałem ten pierwiastek do wolframa i wyszło to samo.
	5		9

Sposób musi być jakiś krótszy, bo takie podnoszenie dwa razy do kwadratu jest żmudne i łatwo można się pomylić.

henrys: r₁+r₂=długość osi wielkiej 2b=3 b=3/2

Benny: Ok będę pamiętał, ale jak z tego wyliczyć długość osi małej?

henrys: 1=√b²−a² w tym przypadku (ogólnie poczytaj o elipsie) 1=9/4−a² a²=5/4

Benny: Ok, dzięki

Mila: F₁=(0,1), F₂=(0,−1) ogniska elipsy. 2c=|F₁F₂|=2 odległość ogniskowa

Benny: Co nam daje ta odległość?

henrys: ja tam źle napisałem, powinno być ogniska to (0,1) i (0,−1) c=odległość ognisk od środka elipsy=√b²−a², a,b osie elipsy r₁+r₂=2b

Mila: c=√a²−b²

Benny: Ok, dziękuje raz jeszcze