funkcja ko(s)miczny wzor samouk: czesc napotkalem pewien spooory problem, probuje rozgyzc teraz suriekcje i iniekcje i ze zrozumieniem szlo nie tak najgorzej, do czasu jednak! wlasnie trafila kosa na kamien juz cieszylem sie ze rozumiem a tu taka niespodzanka moze ktos to rozumie i potrafi przystepnie wytlumaczyc, mamy sprawdzic czy dana funkcja jest suriekcja/ iniekcja: f: R² → R² f(x,y)= (x+y, 2x−y−1) o co wogole chodzi w zapisie tej funkcji?

Edek: A nie czasem źe x wynosi x+y, a y to 2x−y−1?

samouk: oj nie, ale juz chyba rozgryzlem, oto jak sprobuje: przyjme x₁, y₁, x₁, y₂ i porownam f(x₁,y₁) z f(x₂,y₂), a zeby one byly rowne to x₁=x₂ i y₁=y₂ i w ten sposob sprawdze czy tutaj mamy iniekcje? ale jak teraz sprawdzic czy to suriekcja

PW : Dowód różnowartościowości. Weźmy dwie różne pary (x₁,y₁) ≠ (x₂, y₂). Gdyby f(x₁, y₂) = f(x₂, y₂), to byłoby 2x₁−y₁−1 = 2x₂ − y₂ −1 (1) 2(x₁−x₂) = y₁−y₂ i jednocześnie x₁+y₁ = x₂+y₂ (2) x₁−x₂ = −(y₁−y₂). Jeżeli x₁ ≠ x₂ i y₁≠y₂, to można podzielić (1) przez (2) i dostaniemy sprzeczność 2 = −1. Gdyby tylko jedne ze współrzędnych były równe, np. x₁=x₂, to drugie współrzędne też muszą być równe, co wynika zarówno z (1) jak i z (2) (jest to sprzeczność z założeniem (x₁,y₁).≠ (x₂, y₂).

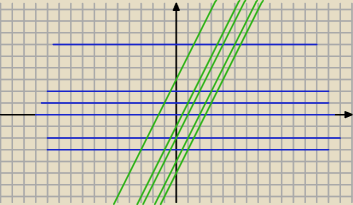
olek: nie wiem co masz do dyspozycji f(x,y)=(x+y,2x−y−1) prostymi równoległymi do osi X pokryjemy całą płaszczyznę R² f(x,0)=(x,2x−1) f(x,1)=(x+1,2x−2) f(x,a)=(x+a,2x−a−1), a∊R f(x,a)=(x+a,g(x+a)) g(x+a)=2x−a−1 g(x)→w[−a,0] ⇒g(x)=2x−3a−1 funkcja liniowa funkcja f(x,y) jest suriekcją ponieważ dla dowolnego ,,a∊R" funkcja g(x+a) pokrywa całą płaszczyznę.

PW : Bez rysowania też można . Mamy udowodnić, że f(x,y) = (a, b) dla dowolnych a, b∊R ma rozwiązanie, czyli że istnieje rozwiązanie układu równań

	⎧	x+y = a
	⎨		.
	⎩	2x−y−1 = b

Wyznacznik główny tego układu jest równy 1·(−1) − 2·1 = − 3. Wyznacznik główny jest różny od zera, czyli rozwiązanie istnieje.