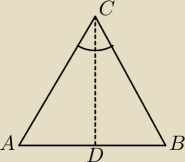
Trojkaty 5-latek: Twierdzenie : W trójkącie równoramiennym kąty przy podstawie sa rowne Dowod : Niech w trojkacie ABCjest |AC|=|BC| prowadzimy dwusieczna CD kąta C . dzieli ona trokat ABC na dwa trojkaty przystające czyli ACD i BCD na mocy cechy (bkb) Teraz pytanie Będą to boki AC i BC oraz CD ? bo musi być kat zawarty miedzy bokami ? Stad kąt A =kątowi B Jakie jeszcze własności trojkata równoramiennego ABC daje jeszcze przystawanie trojkątow ADC I BDC (rysunek

5-latek: Potem jeszcze mam3 zadanka nr 1 Udowodnij ze w trojkacie równoramiennym srodkowe ramion sa rowne nr 2) Udowodnij z ew trojkacie równoramiennym dwusieczne kątow przy podstawie sa rowne nr 3) Udowodnij z ew trójkącie równoramiennym srodkowa poprowadzona do podstawy jest również dwusieczna i wysokoscia Pewnie należy skorzystać z przystawania trojkatow .

5-latek:

Mila: Tak , rysuj, zaznacz równe odcinki i kąty.

5-latek: Dobrze Milu W sobote mam wolne wiec się tym zajme

5-latek: Teraz wlasnie zaczalem przerabiac Figury geometryczne . Przedtem pominalem ten rozdzial

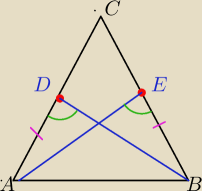
5-latek : No to w takim razie nr z 13:21 Trojkat rownoramienny i AC=BC mamy tu udowodnic ze BD=AE Wiemy ze AD=BE \ ∡BDA=∡AEB Wiemy ze trojkaty ADB i AEB maja maj wspolne ramie AB

5-latek : Nie dopisalem dobrze nr 1 (czyli chodzi o srodkowe

5-latek: Może ktoś to rozpisać ?

Mila: Skąd wiesz , że zielone kąty równe? ∡ABE=∡B AD cecha bkb

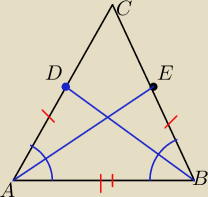
5-latek: Dobry wieczor Milu Wiem z tego ze srodkowa dzieli bok na polowe a tu zalozylem ze AC=BC Teraz AD=BE ∡ABE=∡BAD Teraz na postawie cechy bkb trojkaty ADB i AEB sa przystające i z tego wynika ze AE=BD

Mila: Tak

5-latek: dziekuje Ci Za jakas chwile poproszse Cie o sprawdzenie następnych