rozwiąż nierówność
Mateusz: Rozwiąż nierówność wielomianową
x4−x2+24 ≥ 12(x2−1)
7 paź 17:46
Mila:
x4−x2+24 ≥ 12(x2−1)⇔
x4−x2+24−12x2+12≥0
x4−13x2+36≥0
x2=t, t≥0
t2−13t+36≥0
Dokończysz?
7 paź 18:27
Eta:
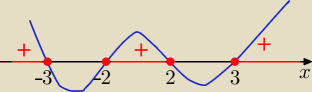
x
4−13x
2+36≥0 ⇒ (x
2−9)(x
2−4)≥0 ⇒ (x−3)(x+3)(x−2)(x+2)≥0
x∊ ............
7 paź 18:32
prosta:
t2−13t+12≥0
(t−1)(1−12)≥0
(x2−1)(x2−12)≥0
(x−1)(x+1)(x−2√3)(x+2√3)≥0
7 paź 18:33
prosta: ups....pomyłka
7 paź 18:34
Eta:
@ prosta
x4−13x2+36≥0
7 paź 18:35
Mateusz: Dziękuję bardzo.
7 paź 18:55
Mateusz: Czy moglibyście jeszcze rozwiązać tą nierówność?
x3−6x2+12x≤8
7 paź 19:03
Mila:
x3−6x2+12x≤8⇔
x3−6x2+12x−8≤0 zwijamy z wzoru skróconego mnożenia
(x−2)3≤0 ⇔ (sprawdź)
x−2<0⇔
x<2
7 paź 21:08
 x4−13x2+36≥0 ⇒ (x2−9)(x2−4)≥0 ⇒ (x−3)(x+3)(x−2)(x+2)≥0
x∊ ............
x4−13x2+36≥0 ⇒ (x2−9)(x2−4)≥0 ⇒ (x−3)(x+3)(x−2)(x+2)≥0
x∊ ............