równania z parametrem Tomek: Witam Wszystkich. Mam taki układ równań : y=|3x+1| 3x+y−m=0 Czy mój tok rozwiązywania jest prawdidłowy : y=|3x+1| y=−3x+m −3x+m=|3x+1| ⇒ −3x+m=3x+1 lub 3x−m=3x+1 Tylko co teraz... Mam zbadać liczbę rozwiązań w zależnosci od parametru m

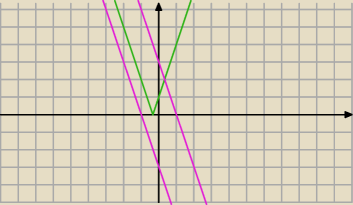
J: Zielony: y = I3x+1I Różowy: y = −3x + m Badaj ile mają punktów wspólych w zależności od m

Tomek: Z wykresu wynika , że w sumie jest tylko jedno rozwiązanie ( 1/3;2).Jeśli podstawię x=1/3 do równań: y=|3x+1| y=−3x+m ⇒ −3x+m=3x+1 ⇒m=3 y=|3x+1| y=−3x+m ⇒ 3x+m=3x+1 ⇒m=1 Czyli rozwiązanie równania jest punkt (1/3;2) dla parametru m=1 i m=3 ? Dziękuje za pomc

J: Dla: m < −1 .... brak rozwiązań Dla: m = − 1 .....nieskończenie wiele Dla: m > −1 ..... dwa rozwiązania

J: ..sorry ... dla m > − 1 oczywiście jedno rozwiazanie

Tomek: Poprawiam błąd y=|3x+1| y=−3x+m −3x+m=3x+1 ⇒m=6x+1 y=|3x+1| y=−3x+m 3x−m=3x+1 ⇒m=−1 Rozumiem już J skąd takie przedziały ale nie wiem gdzie podstawiałeś parametr m aby uzyskać rozwiązania. Proszę o rozpisanie jeśli to nie problem. Dziękuje

J: Popatrz na rysunkek .. jak przesuniesz prostą: y = −3x o jeden w dół ( m = −1) , to pokryje sie ona z lewym ramieniem zielonym ( nieskończenie wiele rozwiazań), jak drgniesz do góry ( m > −1 ) .. jedno rozwiazanie, w dół .. brak rozwiazań

Tomek: Dzięki J, Bardziej obrazowego wyjaśnienia nie mogłem dostać Teraz wszystko jest jasne jak słońce. Miłego dnia życzę!

pigor: ..., analitycznie, widzę to tak : y=|3x+1| i 3x+y−m=0 i (*) y ≥0 ⇒ (y= −3x−1 v y=3x+1) i 3x+y=m ⇔ ⇔ (1) (3x+y= −1 i 3x+y=m) v (2) (3x−y=1 i 3x+y=m) − − 2 układy liniowe o dwóch niewiadomych,gdzie (1) ma ∞ wiele (x,y) i x∊R. y∊R₊, dla m= −1, albo nie ma rozwiązań (sprzeczny) gdy m≠ −1 −−−−−−−−−−−−−−−−−−−−−−−−−−− (2) ma 1 rozwiązanie (x,y) i y ≥0 dla m ≥1, albo 0 rozwiązań , gdy m<1 . ...