wartosc bezwzgledna
5-latek:
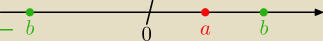
napisz wszystkie nierownosci trojkata dla punktow na osi o wspolrzednych
a,b,0 oraz o wsporzednych a.−b,0
Moze najpierw dla a,b,0
1)|0+a|+|a+b|≥|0+b| czyli |a|+|a+b|≥b
2) |a+b|+|0+b|≥|0+a| czyli |a+b|+|b|≥|a|
Tyle bedzie
7 paź 09:06
5-latek: Chociaz przy pierwszsej nierownosci powinien byc wedlg mnie znak rownosci bo te punkty sa na
osi
7 paź 09:08
5-latek: Bedzie trzecia
3)|0+a|+|0+b|≥|a+b| czyli |a|+|b|≥|a+b|
7 paź 09:12
5-latek: Natomiast dla punktów o wspolrzednych a,−b,0 napisałbym takie
1) |−b+0|+|0+a|=|−b+a| czyli |b|+|a|=|a−b|
2) |0+a|+|−b+a|≥|−b| czyli |a|+|a−b|≥|b|
|−b+0|+|−b+a|≥|0+a| czyli |b|+|a−b|≥a
7 paź 09:36
5-latek: jednej z otrzymanych nierownosci
|a|+|b|≥|a+b| (zapiszse to sobie tak |a+b|≤|a|+|b| używa się przy roznych szacowaniach
Zastosujmy ja do
|a−3|≤1 i |b−3|≤1
czemu teraz |a−b|≤2
7 paź 09:59
5-latek: No dobrze .
To podstawiam do wzoru
|a−3+b−3|≤1+1 bo wartość bezwzgledna |a−3| jest mniejsza rowma 1 i to samo |b−3| jest
mniejsza rowna 1 wiec według wzoru je dodajemy no ale wtedy mam
|a+b−6|≤2
7 paź 10:26
Alek: dlatego, że obydwie liczby a i b należą do przedziału <2,4> więc ich odległość |a−b|≤2 (tyle
wynosi długość tego przedziału)
7 paź 10:50
5-latek: OK

7 paź 11:04
5-latek: Milu 
Sprawdzisz mi te nierownosci ?
7 paź 23:19
5-latek:
8 paź 00:03
Mila:
Witam i dobranoc.
Jutro sprawdzę, dziś miałam mało czasu na zadania z forum, tylko dorywczo.

8 paź 00:23
5-latek: Dobrze
Dobranoc

8 paź 00:43
5-latek: Przypomne się
Milu 
8 paź 22:47
Mila:
1) Przykład zastosowania

a|+|b|≥|a+b|
Obliczyć najmniejszą wartość wyrażenia: |x−4|+|x+2|
|x−4|+|x+2|=|x−4|+|−x−2|≥|x−4+(−x−2)|=|6|=6
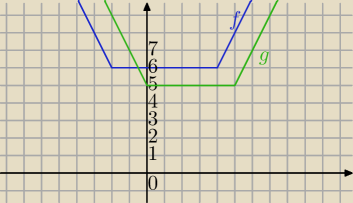
Sprawdzimy, co pokaże wykres:
f(x)=|x−4|+|x+2|
2)
a) 9:36
|−b+0|+|0+a|=|a|+|b|
pozostałe dwie dobrze.
b)|a|+|a−b|≥|b|
Przykład:
|x|+|x−5|=|−x|+|x−5|≥|−x+x−5|=|−5|=5
g(x)=|x|+|x−5|
8 paź 23:10
5-latek: Również za to dziekuje

8 paź 23:13
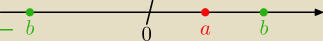 napisz wszystkie nierownosci trojkata dla punktow na osi o wspolrzednych
a,b,0 oraz o wsporzednych a.−b,0
Moze najpierw dla a,b,0
1)|0+a|+|a+b|≥|0+b| czyli |a|+|a+b|≥b
2) |a+b|+|0+b|≥|0+a| czyli |a+b|+|b|≥|a|
Tyle bedzie
napisz wszystkie nierownosci trojkata dla punktow na osi o wspolrzednych
a,b,0 oraz o wsporzednych a.−b,0
Moze najpierw dla a,b,0
1)|0+a|+|a+b|≥|0+b| czyli |a|+|a+b|≥b
2) |a+b|+|0+b|≥|0+a| czyli |a+b|+|b|≥|a|
Tyle bedzie

 Sprawdzisz mi te nierownosci ?
Sprawdzisz mi te nierownosci ?



 1) Przykład zastosowania
1) Przykład zastosowania a|+|b|≥|a+b|
Obliczyć najmniejszą wartość wyrażenia: |x−4|+|x+2|
|x−4|+|x+2|=|x−4|+|−x−2|≥|x−4+(−x−2)|=|6|=6
Sprawdzimy, co pokaże wykres: f(x)=|x−4|+|x+2|
2)
a) 9:36
|−b+0|+|0+a|=|a|+|b|
pozostałe dwie dobrze.
b)|a|+|a−b|≥|b|
Przykład:
|x|+|x−5|=|−x|+|x−5|≥|−x+x−5|=|−5|=5
g(x)=|x|+|x−5|
a|+|b|≥|a+b|
Obliczyć najmniejszą wartość wyrażenia: |x−4|+|x+2|
|x−4|+|x+2|=|x−4|+|−x−2|≥|x−4+(−x−2)|=|6|=6
Sprawdzimy, co pokaże wykres: f(x)=|x−4|+|x+2|
2)
a) 9:36
|−b+0|+|0+a|=|a|+|b|
pozostałe dwie dobrze.
b)|a|+|a−b|≥|b|
Przykład:
|x|+|x−5|=|−x|+|x−5|≥|−x+x−5|=|−5|=5
g(x)=|x|+|x−5|
