Dla jakich argumentów, funkcja F(x)=x+3/x-2 przyjmuje wartości większe niż funkc Nieobecny: Dla jakich argumentów, funkcja F(x)=x+3/x−2 przyjmuje wartości większe niż funkcja G(x)=x−5/x+2? Rozumiem że F(x)>G(x), ale potem jakieś bzdury wychodzą, a nie było mnie na lekcji z tym przykładem zadania.

Janek191:

x + 3		x − 5
	>		; x ≠ − 2 i x ≠ 2
x −2		x + 2

x + 3		x −5
	−		> 0
x −2		x + 2

Sprowadź do wspólnego mianownika i wykonaj odejmowanie

Eta:

	x+3		x−5
f(x)>g(x) ⇒		>		, x≠2 , x≠ −2
	x−2		x+2

(x+3)(x+2)−(x−5)(x−2)		12x−4
	>0 ⇒		>0
(x−2)(x+2)		(x−2)(x+2)

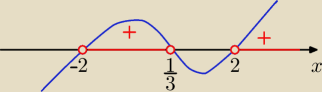
4(3x−1)(x−2)(x+2)>0

	1
Odp: x∊(−2,		) U (2,∞)
	3

Janek191:

Nieobecny: Dziękuję bardzo. Jeszcze taki problem z zadaniem: Dla jakich argumentów funkcja F(x)=x+3/x−2 przyjmuje wartości większe niż funkcja G(x)=x−5/x+2

Nieobecny: Sorki przepisałem zły przykład Chodziło mi o to: Wyznacz argument, dla którego funkcja homograficzna F przyjmuje obok podaną wartość jeśli F(x)=x+1/x−1, w=2+√3

Eta: x=√3

	√3+1
bo f(√3)=		= ...=2+√3
	√3−1

Nieobecny: Eta, tylko jak do tego dojść pisemnie? Będę wdzięczny

Eta:

x+1
	=2+√3 , x≠1
x−1

x+1=(2+√3)(x−1) ⇒ x+1=(2+√3)x −2−√3 ⇒ (2+√3−1)x= 2+√3+1 (√3+1)x=3+√3 /* (√3−1) 2x=(3+√3)(√3−1) ⇒ ................ x= √3