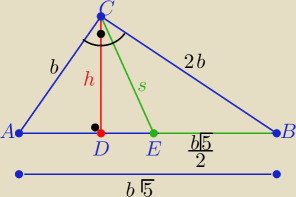
Planimetria dominika: W trojkącie prostokątnym ABC z wierzchołka kąta prostego poprowadzono wysokość CD i środkową CE. oblicz stosunek ^|CD|_|CE|, jeśli wiadomo, że stosunek przyprostokątnych jest równy 1:2. PrzyprostOkatna krótsza = b Przyprostokątna dłuższa = 2b Z twierdzenia Pitagorasa przeciwprostokątna = √5 b Pole trojkata abc wyszło mi równe b² Następnie liczyłam wysokość ze wzoru znów na pole ABC tylko podstawa była tym raEm

	b √5
przeciwprostokątna i h czyli szukana wysokość , h wyszło mi
	5

Proszę o dalsza pomoc

dominika: Pomoże ktoś ?

dominika: ?

Eta:

	1		√5b
|AB|=√b2+4b2= √5b to s=|CE|=		|AB|=
	2		2

	2b*b		2b
h=		=
	|AB|		√5

|CD|		2b		2		4
	=		*		=
|CE|		√5		√5b		5

dominika: Skad wiemy ze S= 1/2 AB

Eta:

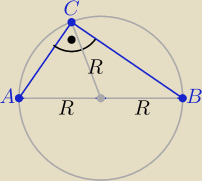
pigor: ..., powyżej pani η narysowała i opisała co trzeba Maju, prosisz jednak, to masz, powtórzę, a więc patrz i myśl, otóż w Δ prostokątnym długość środkowej przeciwprostokątnej to jej połowa jako długość promienia okręgu opisanego na Δ prostokątnym, (kąt wpisany w okrąg oparty na średnicy jest prosty) czyli tu: |CE|=¹₂|AB|=¹₂√5b, a z pola ΔABC |CD|*√5b=b*2b ⇒ ⇒ 5|CD|= 2√5b, stąd szukany stosunek (iloraz) :

|CD|		25√5b		2		2		4
	=		=		*		=		=0,8..
|CE|		12√5b		5		1		5

dobranoc.