Optymalizacja - prostopadłościan. KeramxD: 1. Suma długości prostopadłościanu z jednego wierzchołka wynosi 6. Jedna krawędź jest dwa razy większa od drugiej. Wyznacz wymiary prostopadłościanu tak aby objętość była najwieksza.

Mila: Suma długości krawędzi? prostopadłościanu ? Która krawędź ? Napisz precyzyjnie treść.

KeramxD: Krawędzi, uciekło mi. Powinno byc długości prostopadłościanu.

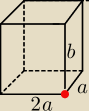
Mila: 2a+a+b=6 3a+b=6⇔b=6−3a >0 6>3a 0<a<2 V=2a*a*b V(a)=2a²*(6−3a)=12a²−6a³ V'(a)=24a−18a² 24a−18a²=0/:6 4a−3a²=0 a(4−3a)=0

	4
a=0 nie odp.war. zad. lub a=
	3

a(4−3a)>0

	4
a∊(0,		)
	3

	4
Przy przejściu przez punkt (		,0) pochodna zmienia znak z z dodatniego na ujemny⇔
	3

	4
w a=		ma maksimum
	3

	4
a=
	3

	8
2a=
	3

b=2