Nie mam pojęcia, jak się za to zabrać. Funkcja liniowa Paulina: Dana jest funkcja f(x) = Ix−1I + I2 − xI. Określ liczbę rozwiązań równania: f(x) = m, w zależności od parametru m.

olekturbo: Narysuj taką funkcję i w zależności ile prosta m ma punktów wspólnych z tą prosta taki przyjmuje wynik

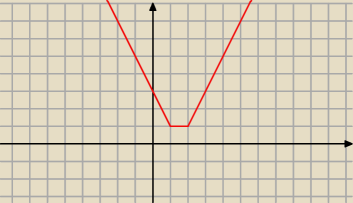
bezendu: m∊(−∞,1) brak rozwiązań m∊{1} nieskończenie wiele rozwiązań m∊(1,∞) dwa rozwiązania

Paulina: Tylko jest taki problem, że nauczycielka nie pozwala rysować do tego typu zadań wykresów.

PW: No to walnij tak: Znana jest nierówność: dla dowolnych a,b∊R |a| + |b| ≥ |a + b|, przy czym równość ma miejsce wtedy i tylko wtedy, gdy ab ≥ 0. Po zastosowaniu tej nierówności dla a = x − 1 i b = 2 − x otrzymujemy |x − 1| + |2 − x| ≥ |x − 1 + 2 − x|, czyli (1) |x − 1| + |2 − x| ≥ 1, przy czym równość ma miejsce wtedy i tylko wtedy, gdy (x − 1) (2 − x) ≥ 0, to znaczy gdy x∊<1, 2>. Odpowiedź już prawie jest: 1. wartości funkcji po lewej stronie badanego równania (2) |x − 1| + |2 − x| = m są równe 1 dla x∊<1, 2>, jeżeli więc m = 1, to rozwiązaniem równania (2) jest każda liczba z tego przedziału (czyli dla m = 1 jest nieskończenie wiele rozwiązań). 2. wartości funkcji po lewej stronie są większe od 1 dla pozostałych x, a więc jeśli m < 1, to rozwiązań nie ma. 3. dla m > 1 istnieją dwa rozwiązania równania (2), co wynika z faktu, że jeśli (2) ma rozwiązanie x₀, to również 3 − x₀ jest rozwiązaniem, co łatwo sprawdzić; istnienie tylko jednego rozwiązania dla x > 2 jest oczywiste, gdyż dla takich x równanie (2) jest równaniem liniowym, a w konsekwencji drugie rozwiązanie też istnieje i nie ma ich więcej, bo dla x < 1 równanie (2) też jest równaniem liniowym. To był dowcip. Pani profesor na pewno wymaga, by rozpatrywać badane równanie na trzech przedziałach: (−∞,1), <1, 2) oraz <2,∞). Taki podział wynika w sposób naturalny z tego, że wyrażenia "między kreseczkami modułów" stają się dodatnie lub ujemne po przekroczeniu krańców tych przedziałów, a więc można te wyrażenia zapisać bez modułów korzystając z definicji (dla wartości nieujemnych pozostawiamy jak były, a dla ujemnych zmieniamy znak). Otrzymujemy na każdym z przedziałów inne równanie, trzeba je po prostu rozwiązać. Można to spokojnie zrobić bez rysowania wykresu. Prawdę mówiąc wykres powinien (może) być ilustracją, a nie metodą, Pani profesor ma rację.