nierówność z parametrem Zadaniowiec: Witam, co ja tutaj wykonuje źle? Znajdź te wartości parametru m, dla których liczba 2 nie należy do zbioru rozwiązań nierówności x²+(m³+3)x−6m²−18m+44 > 0 tak więc f(2)≤0 4+2m³+6−6m²−18m+44≤0 2m³−6m²−18m+54≤0 3 jest pierwiastkiem, więc: (m−3)(2m²−18)≤0 m=3 v m=−3 v m=3 no więc z wykresu np. można wyczytać, że m∊ <−3, 3> (tylko ten przedział jest pod osią) w odpowiedzi jest: m∊(−∞, −3) v {3}

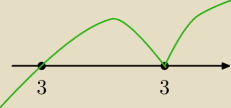
J: dla: x = 3 ..masz punkt odbicia na wykresie

J: m ∊ (−∞,3> U {3}

J: m ∊ (−∞ , −3 > U {3}

Zadaniowiec: ajj racja, dziękuję, bo zapomniałem o tym i próbowałem w jakiś dziwny sposób to rozwiązać ale skoro (m−3) −> m=3 jest pierwiastkiem jednokrotnym, to czy przy "3" na osi nie powinno przeciąć osi?