Nierówność z wartością bezwzględną
Janusz: Narysuj wykres funkcji:
|x−y| + |x| − |y| ≤ 2
Jak się za to zabrać?
Jakby nie było |x−y| to bym to rozbił na cztery możliwości − każdą ćwiartkę układu, ale jak
mamy |x−y|, to najpierw zakładam, ze?
x−y≥0
x≥0
i co dalej?
4 paź 22:44
5-latek: |x−y|≤|x|+|y|
4 paź 22:46
PW: Chłopie, o co Ty pytasz? Jaki wykres funkcji?
4 paź 22:53
Janusz: Przepraszam... Polcenie brzmiało tylko "Narysuj:"
Co do tego, co napisał 5−latek.
Czyli:
|x−y| ≤ −|x| + |y| + 2

Co dalej?
|x−y| ≤ − |x+y| +2 ?
5 paź 00:41
Godzio:
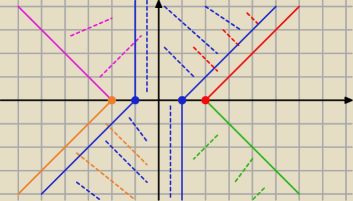
|x − y| ≤ 2 + |y| − |x|
Żeby nierówność miała sens musi być spełniony warunek
2 + |y| − |x| ≥ 0 ⇒ |x| − |y| ≤ 2 −− to jest nasz obszar, w którym możemy cokolwiek rysować.
Aby to narysować rozważamy 4 przypadki
x,y ≥ 0
y ≥ x − 2
x ≥ 0 i y < 0
y ≤ − x + 2
x < 0 i y ≥ 0
y ≥ − x − 2
x < 0 i y < 0
y ≤ x + 2
Z definicji:
x − y ≤ 2 + |y| − |x| i x − y ≥ −2 − |y| + |x|
Rozważamy 4 przypadki
1
o x ≥ 0 i y ≥ 0
x − y ≤ 2 + y − x i x − y ≥ − 2 − y + x
y ≥ x − 1 i 0 ≥ − 2
2
o x ≥ 0 i y < 0
x − y ≤ 2 − y − x i x − y ≥ − 2 + y + x
x ≤ 1 i y ≤ 1
3
o x < 0 i y ≥ 0
x − y ≤ 2 + y + x i x − y ≥ − 2 − y − x
y ≥ − 1 i x ≥ −1
4
o x < 0 i y < 0
x − y ≤ 2 + −y + x i x − y ≥ −2 + y − x
0 ≤ 2 i y ≤ x + 1
To co na niebiesko to kolejne krzywe, zaraz narysuje tylko obszar z odpowiedzi, żeby nie było
wątpliwości.
5 paź 01:05
Godzio:
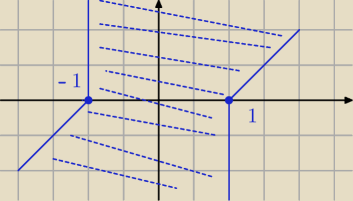
5 paź 01:07
Janusz: Dziękuję bardzo, już załapałem

5 paź 10:50
 Co dalej?
|x−y| ≤ − |x+y| +2 ?
Co dalej?
|x−y| ≤ − |x+y| +2 ?
 |x − y| ≤ 2 + |y| − |x|
Żeby nierówność miała sens musi być spełniony warunek
2 + |y| − |x| ≥ 0 ⇒ |x| − |y| ≤ 2 −− to jest nasz obszar, w którym możemy cokolwiek rysować.
Aby to narysować rozważamy 4 przypadki
x,y ≥ 0
y ≥ x − 2
x ≥ 0 i y < 0
y ≤ − x + 2
x < 0 i y ≥ 0
y ≥ − x − 2
x < 0 i y < 0
y ≤ x + 2
Z definicji:
x − y ≤ 2 + |y| − |x| i x − y ≥ −2 − |y| + |x|
Rozważamy 4 przypadki
1o x ≥ 0 i y ≥ 0
x − y ≤ 2 + y − x i x − y ≥ − 2 − y + x
y ≥ x − 1 i 0 ≥ − 2
2o x ≥ 0 i y < 0
x − y ≤ 2 − y − x i x − y ≥ − 2 + y + x
x ≤ 1 i y ≤ 1
3o x < 0 i y ≥ 0
x − y ≤ 2 + y + x i x − y ≥ − 2 − y − x
y ≥ − 1 i x ≥ −1
4o x < 0 i y < 0
x − y ≤ 2 + −y + x i x − y ≥ −2 + y − x
0 ≤ 2 i y ≤ x + 1
To co na niebiesko to kolejne krzywe, zaraz narysuje tylko obszar z odpowiedzi, żeby nie było
wątpliwości.
|x − y| ≤ 2 + |y| − |x|
Żeby nierówność miała sens musi być spełniony warunek
2 + |y| − |x| ≥ 0 ⇒ |x| − |y| ≤ 2 −− to jest nasz obszar, w którym możemy cokolwiek rysować.
Aby to narysować rozważamy 4 przypadki
x,y ≥ 0
y ≥ x − 2
x ≥ 0 i y < 0
y ≤ − x + 2
x < 0 i y ≥ 0
y ≥ − x − 2
x < 0 i y < 0
y ≤ x + 2
Z definicji:
x − y ≤ 2 + |y| − |x| i x − y ≥ −2 − |y| + |x|
Rozważamy 4 przypadki
1o x ≥ 0 i y ≥ 0
x − y ≤ 2 + y − x i x − y ≥ − 2 − y + x
y ≥ x − 1 i 0 ≥ − 2
2o x ≥ 0 i y < 0
x − y ≤ 2 − y − x i x − y ≥ − 2 + y + x
x ≤ 1 i y ≤ 1
3o x < 0 i y ≥ 0
x − y ≤ 2 + y + x i x − y ≥ − 2 − y − x
y ≥ − 1 i x ≥ −1
4o x < 0 i y < 0
x − y ≤ 2 + −y + x i x − y ≥ −2 + y − x
0 ≤ 2 i y ≤ x + 1
To co na niebiesko to kolejne krzywe, zaraz narysuje tylko obszar z odpowiedzi, żeby nie było
wątpliwości.

