Nierówność z wartością bezwzględną
Mefju: Witam, mam problem z pewnym zadaniem ponieważ nie wiem czy dobrze je rozwiązałem.
Mamy taką o to nierówność: |x−2| − |x| < 4
Wymieniłem sobie 3 przedziały gdzie: 1. x∊(−∞;0) 2.x∊<0;2) 3.x∊<2;∞)
Według moich wyników wychodzi, że: 1. 2<4 2. x>−1 3.−2<4.
Czy jest to dobrze i czy moglibyście pokazać najlepsze sposoby na rozwiązanie takich
nierówności?
Zarówno tam gdzie są dwa bezwzględne obok siebie oraz gdzie jeden jest w drugim.
4 paź 21:47
5-latek: Jeśli masz dwie lub więcej wartości bezwzględnych to przedzialy
4 paź 21:54
5-latek: Pokaz najlepiej obliczenia
4 paź 21:58
Janek191:
Poczytaj sobie po lewej stronie : wartość bezwzględna
4 paź 21:59
Mefju: no przy tych przedziałach co wymieniłiem to mam takie obliczenia
1. −x+2+x < 4 skróciłem "iksy" to wynik jak powyżej
2. −x+2−x < 4 potem −2x < 2 już po przeniesieniu i dodaniu, podzieliłem, wynik wyżej
3. x−2−x < 4 no to wynik jak w pierwszym poście, w sumie nie dużo obliczeń.
4 paź 22:01
PW: W tym wypadku
|x − 2| < |x| + 4
− obie strony nieujemne, nierówność jest więc równoważna następującej:
x 2 − 4x + 4 < x2 + 8|x| + 16
− x + 1 < 2|x| + 4
− x < 2|x| + 3
− dla dodatnich x i zera prawdziwa w sposób oczywisty, dla ujemnych x ma postać
− x < −2x + 3 , x∊(−∞, 0)
x < 3, x∊(−∞, 0),
rozwiązaniami tej nierówności też są wszystkie x z dziedziny.
4 paź 22:04
Mila:
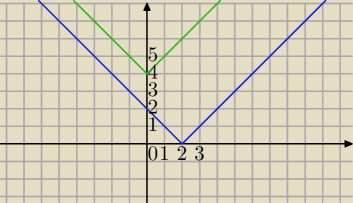
Możesz też tak:
Metoda graficzna:
|x−2| − |x| < 4⇔
|x−2|<|x|+4
f(x)=|x−2|
g(x)=|x|+4
Wykres f(x) leży poniżej wykresu funkcji g(x) dla każdego x∊R
Metoda algebraiczna
1)|x−2|=x−2 dla x≥2
2)|x|=x dla x≥0
♦x∊(−
∞,0) wtedy mamy nierówność:
−x+2−(−x)<4⇔−x+2+x<4⇔2<4 Prawda⇔spełniona nierówność dla każdego x∊(−
∞,0)
♦x∊<0,2) wtedy mamy nierówność:
−x+2−x<4
−2x<2
x>−1 ⇔spełniona nierówność dla x∊<0,2)
♦x∊<2,
∞) wtedy mamy nierówność:
x−2−x<4
−2<4 prawda, spełniona nierówność dla każdego x∊<2,
∞)⇔
|x−2| − |x| < 4 dla każdego x∊R
4 paź 22:07
Mefju: Dzięki PW jednak w odpowiedziach mam podane, że x∊R chyba,że czegoś nie zrozumiałem z twojej
odpowiedzi.
4 paź 22:08
5-latek: No to teraz należy wyznaczyć rozwiązanie
Patrz uważnie na przedzialy
4 paź 22:08
5-latek: Już masz
4 paź 22:10
Mefju: Dzięki Mila! Czyli w sumie nie miałem źle tylko kwestia zapisania na końcu obliczeń,
że nierówność jest prawdziwa dla tych rozwiązań. Dzięki raz jeszcze!
4 paź 22:11
PW: N ie zrozumiałeś. Specjalnie napisałem w ostatnim zdaniu
rozwiązaniami tej nierówności też są wszystkie x z dziedziny.
4 paź 22:15
Mefju: A mógłbym jeszcze cię prosić o obliczenie tego zadania: |x+5|−|x−2| ≤ 3
Za cholere nie chce mi wyjść poprawny wynik. Będę wdzięczny.
4 paź 22:18
Mila:
Mefju, właśnie o to chodzi, że nie napisałeś odpowiedzi.
Nierówność jest spełniona dla każdego x∊R, albo tak jak podał PW,
jeśli zostawisz tylko tak, jak napisałeś pierwszym wpisie, to obetną Ci punkty na maturze i
klasówce też.
4 paź 22:21
Mila:

|x+5|−|x−2| ≤ 3
|x+5|=x+5 dla x≥−5
|x−2|=x−2 dla x≥2
−−−−−−−−−−−−−−−−−−−−
1)
x<−5 wtedy mamy nierówność:
−x−5−(−x+2)≤3
−x−5+x−2≤3
−7≤3 prawda, nierówność spełniona dla każdego x∊(−
∞,−5)
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
lub
2) x∊<−5,2)
x+5−(−x+2)≤3
x+5+x−2≤3
2x≤0⇔x∊<−5,0>
lub
3) x∊<2,
∞)
x+5−(x−2)≤3
x+5−x+2≤3
7≤3 fałsz , brak rozwiązania w tym przedziale
====================
odp.
x∊(−
∞,0>
4 paź 22:35
 Możesz też tak:
Metoda graficzna:
|x−2| − |x| < 4⇔
|x−2|<|x|+4
f(x)=|x−2|
g(x)=|x|+4
Wykres f(x) leży poniżej wykresu funkcji g(x) dla każdego x∊R
Metoda algebraiczna
1)|x−2|=x−2 dla x≥2
2)|x|=x dla x≥0
♦x∊(−∞,0) wtedy mamy nierówność:
−x+2−(−x)<4⇔−x+2+x<4⇔2<4 Prawda⇔spełniona nierówność dla każdego x∊(−∞,0)
♦x∊<0,2) wtedy mamy nierówność:
−x+2−x<4
−2x<2
x>−1 ⇔spełniona nierówność dla x∊<0,2)
♦x∊<2,∞) wtedy mamy nierówność:
x−2−x<4
−2<4 prawda, spełniona nierówność dla każdego x∊<2,∞)⇔
|x−2| − |x| < 4 dla każdego x∊R
Możesz też tak:
Metoda graficzna:
|x−2| − |x| < 4⇔
|x−2|<|x|+4
f(x)=|x−2|
g(x)=|x|+4
Wykres f(x) leży poniżej wykresu funkcji g(x) dla każdego x∊R
Metoda algebraiczna
1)|x−2|=x−2 dla x≥2
2)|x|=x dla x≥0
♦x∊(−∞,0) wtedy mamy nierówność:
−x+2−(−x)<4⇔−x+2+x<4⇔2<4 Prawda⇔spełniona nierówność dla każdego x∊(−∞,0)
♦x∊<0,2) wtedy mamy nierówność:
−x+2−x<4
−2x<2
x>−1 ⇔spełniona nierówność dla x∊<0,2)
♦x∊<2,∞) wtedy mamy nierówność:
x−2−x<4
−2<4 prawda, spełniona nierówność dla każdego x∊<2,∞)⇔
|x−2| − |x| < 4 dla każdego x∊R
 |x+5|−|x−2| ≤ 3
|x+5|=x+5 dla x≥−5
|x−2|=x−2 dla x≥2
−−−−−−−−−−−−−−−−−−−−
1)
x<−5 wtedy mamy nierówność:
−x−5−(−x+2)≤3
−x−5+x−2≤3
−7≤3 prawda, nierówność spełniona dla każdego x∊(−∞,−5)
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
lub
2) x∊<−5,2)
x+5−(−x+2)≤3
x+5+x−2≤3
2x≤0⇔x∊<−5,0>
lub
3) x∊<2,∞)
x+5−(x−2)≤3
x+5−x+2≤3
7≤3 fałsz , brak rozwiązania w tym przedziale
====================
odp.
x∊(−∞,0>
|x+5|−|x−2| ≤ 3
|x+5|=x+5 dla x≥−5
|x−2|=x−2 dla x≥2
−−−−−−−−−−−−−−−−−−−−
1)
x<−5 wtedy mamy nierówność:
−x−5−(−x+2)≤3
−x−5+x−2≤3
−7≤3 prawda, nierówność spełniona dla każdego x∊(−∞,−5)
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
lub
2) x∊<−5,2)
x+5−(−x+2)≤3
x+5+x−2≤3
2x≤0⇔x∊<−5,0>
lub
3) x∊<2,∞)
x+5−(x−2)≤3
x+5−x+2≤3
7≤3 fałsz , brak rozwiązania w tym przedziale
====================
odp.
x∊(−∞,0>