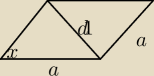
romb olekturbo: Oblicz długości przekątnych rombu o bokach długości a i cosinusie kąta ostrego = 1/4

	1
cosx =
	4

P = 2 * 1/2 * a * a * sinx sin²x + cos²x = 1

	1
sin2x +		= 1
	16

	15
sin2x =
	16

	√15
sinx =
	4

	√15		√15
P = 2*1/2 * a * a *		=		* a2
	4		4

d1 = a² + a² − 2a²cosx

	1
d1 = 2a2 − 2a2 *
	4

	3
d1 =		a2
	2

1		√15
	d1d2 =		* a2
2		4

1		3		√15
	*		a2 * d2 =		* a2
2		2		4

3d2 = √15

	√15
d2 =
	3

da się to zrobić łatwiej?

Janek191: Tam powinno być d₁² = ...

olekturbo: nie podnioslem d1 do kwadratu... ale czy i tak da sie to zrobic latwiej?

5years old: Mysle ze dwa razy twierdzenie cosinusow i po zabawie

olekturbo: a jezeli cosα = 1/4 to skąd mam znaleźc cosβ. cos(180−α) ?

5years old: tak

Eta:

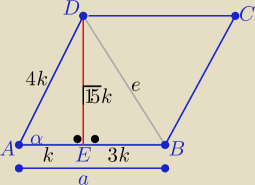
	1
|AC|=f , |BD|=e , |AB|=a i cosα=
	4

to: |AE|=k , AD|=AB|=4k to |DE|=√15k , k>0 |EB|=3k i e= √15k²+9k²= 2√6k

	a
|AB|=4k =a ⇒ a=
	4

	√6		3		5
e=		a oraz e2+f2=4a2 ⇒ f2=4a2−		a2=		a2
	2		2		2

	√10
f=		a
	2

Eta:

	a
Poprawiam zapis : |AB|=4k=a ⇒k=
	4