Różnowartościowość funkcji
monikaaa11: Zbadaj różnowartościowość funkcji dane wzorem y=f(x). Jeśli jest to funkcja różnowarosciowa
znajdź do niej funkcje odwrotną.
f(x)= 2x+53x−6
Mam podane że do rozwiązania potrzebne są takie kroki:
1. Df
2. Df−1
3. Czy funkcja jest różnowartościowa?
4. f−1
4 paź 16:52
5-latek: | | 2x+5 | | 3 | | 2 | |
f(x)= |
| = |
| + |
| |
| | 3x−6 | | x−2 | | 3 | |
Teraz już powinno być latwiej
4 paź 17:26
Janek191:
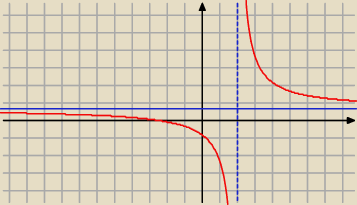
4 paź 17:43
5-latek: Czesc

4 paź 17:44
Janek191:
1) Df = ℛ \ { 2}
4 paź 17:44
Janek191:
Cześć 5 − latku

4 paź 17:45
5-latek: No zobaczymy czy się panna odezwie
4 paź 17:50
Janek191:
NIech x
1 < x
2 < 2 ⇒ x
1 − x
2 < 0
| | 3 | | 2 | | 3 | | 2 | |
f(x1) − f(x2) = |
| + |
| − [ |
| + |
| ] = |
| | x1 − 2 | | 3 | | x2 − 2 | | 3 | |
| | 3 | | 3 | |
= |
| − |
| > 0 czyli f jest malejąca w ( − ∞ ; 2) |
| | x1 − 2 | | x2 − 2 | |
Podobnie
2 < x
1 < x
2 ⇒ x
1 − x
2 < 0
f(x
1) − f(x
2) = .... > 0 czyli f jest malejąca w ( 2; +
∞ )
Po zamianie zmiennych:
| | 9 | |
y = f−1 (x) = |
| + 2 |
| | 3 x − 2 | |
D
f−1 = ℛ \
23
4 paź 18:02
Janek191:
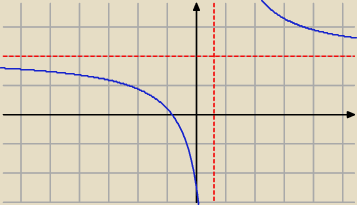
4 paź 18:06
5-latek: Ciagnie Cie jednak na zadane.pl

A panna dalej się nie odzywa
4 paź 18:11
Janek191:
Pewnie poszła na spacer z pieskiem ?

4 paź 18:28
monikaaa11: Na spacer z pieskiem nie poszłam, ale dzięki za pomoc

Jednak nie za bardzo mi to pomogło.
Potrzebuje rozwiązania, ale nie graficznego. Chciałam wstawić tutaj zdjęcie z wykładów,ale nie
wiem jak. Tam robiliśmy zupełnie inaczej, ale nie wiem co się skąd wzięło
4 paź 20:14
Janek191:
Wykresy są podane dodatkowo

Funkcja malejąca jest różnowartościowa.
4 paź 20:19
PW: Nie mogliście robić tego zupełnie inaczej, Janek191 wszystko wyjaśnił − i
różnowartościowość, i sposób szukania wzoru na funkcję odwrotną.
4 paź 20:30




 A panna dalej się nie odzywa
A panna dalej się nie odzywa

 Jednak nie za bardzo mi to pomogło.
Potrzebuje rozwiązania, ale nie graficznego. Chciałam wstawić tutaj zdjęcie z wykładów,ale nie
wiem jak. Tam robiliśmy zupełnie inaczej, ale nie wiem co się skąd wzięło
Jednak nie za bardzo mi to pomogło.
Potrzebuje rozwiązania, ale nie graficznego. Chciałam wstawić tutaj zdjęcie z wykładów,ale nie
wiem jak. Tam robiliśmy zupełnie inaczej, ale nie wiem co się skąd wzięło
 Funkcja malejąca jest różnowartościowa.
Funkcja malejąca jest różnowartościowa.