środek symetrii
Funji: Hej. Mam takie pytanie. W piątek miałem poprawę sprawdzianu z symetrii i było takie zadanie:
"Środkiem symetrii kwadratu jest punkt (0,0). Jeden z jego wierzchołków ma współrzędne (3,4).
Znajdź współrzędne pozostałych wierzchołków i narysuj ten kwadrat."
Czy współrzędne pozostałych wierzchołków to: (−3,−4), (−3,4) i (3,−4)?
4 paź 14:09
sushi_gg6397228:
zaznacz te punkty w układzie i
sprawdź czy masz kąty proste miedzy bokami oraz czy boki maja jednakowa długość
4 paź 14:11
Funji: właśnie nie mają tej samej długości. Dlatego nie wiem co zrobiłem źle
4 paź 14:12
henrys:
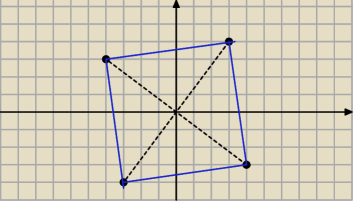
4 paź 14:14
Funji: jak to zrobiłeś?
4 paź 14:16
PW: Założyłeś niesłusznie, że boki są równoległe do osi (nie ma takiego założenia w treści
zadania)i. Trzeba było przekształcić symetrycznie podany wierzchołek (dostałbyś drugi −
położony "po przekątnej") i myśleć o pozostałych.
4 paź 14:16
Funji: faktycznie.Dzięki wielkie
4 paź 14:17
PW: Nie widziałem rysunku, uwaga dotyczyła pierwszego pytania.

4 paź 14:17
henrys: tak jak napisał PW
4 paź 14:17
sushi_gg6397228:
jak masz podany np wierzchołek A, to liczysz C, ze wzory na srodek odcinka
2. wzor na prosta AC ...
3. prosta prostopadla do AC i przechodzaca przez O(0;0) prosta DO: y= a1x+b1
potem porownać długości |AO|= |DO| gdzie D(x, a1 x +b1)
4 paź 14:17
Funji: ok. super. jestem w 2 gimnazjum. nie znam tych wzorów
4 paź 14:20
Bogdan:
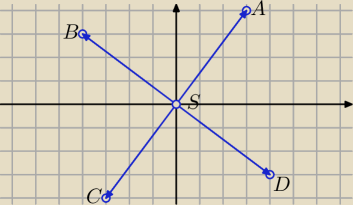
Można skorzystać z wektorów
SA
→ = [p, q]
SB
→ = [−q, p]
SC
→ = [−p, −q]
SD
→ = [q, −p]
4 paź 14:39
Funji: jest jakiś inny sposób oprócz "kombinowania" ?
4 paź 14:39
Bogdan:
A = (3, 4), S = (0, 0)
w tym przypadku SA→ = [3 − 0, 4 − 0] = [3, 4], p=3, q = 4
4 paź 14:40
Funji: nadal nie rozumiem

4 paź 14:40
Funji: dlaczego SB ma −q,p?
4 paź 14:41
Bogdan:
to wynika z prostopadłości wektorów, ale tego materiału nie omawia się w gimnazjum
4 paź 14:45
Bogdan:
wektory w→= [a, b] i v→= [c, d] są prostopadle wtedy, gdy ac + bd = 0
4 paź 14:49
Funji: a korzystając z tego co miałem na lekcji czy narysowanie symetralnej boku AC i zaznaczenie jej
tak, aby boki były takiej samej długo by wystarczyło?
4 paź 14:51
PW: Nie wiem jak uczeń gimnazjum powinien postępować. Moja propozycja jest taka jak o 14:16 −
powinien wiedzieć, że obrazem punktu (3, 4) jest punkt (−4, −3) − taki wzór na pewno był.
Mając końce przekątnej obliczy kwadrat jej długości:
d2 = (3+4)2 + (4+3)2 = 2·72,
a korzystając z twierdzenia Pitagorasa wyliczy długość boku:
a2 + a2 = d2
2a2. = d2
zatem
a = 7.
Mając długość boku cyrklem wyznaczy pozostałe wierzchołki kreśląc okręgi o środku (3,4) i
promieniu 7 oraz o środku (−4, −3) i promieniu 7. Współrzędne wierzchołków po prostu odczyta z
rysunku.
4 paź 14:54
henrys:
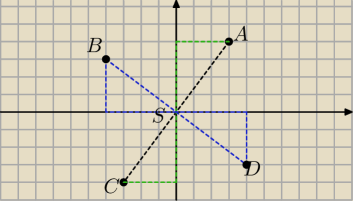
może ten rysunek Ci pomoże?
AC jest przekątną Twojego kwadratu, obracasz zielony trójkąt o 90
. Wierzchołek A przejdzie na
kolejny wierzchołek kwadratu.
4 paź 15:03
Funji: narysowałem symetralną i okrąg o środku w (0,0) i promieniu SA. Punkty przecięcia okręgu i
symetralnej są pozostałymi wierzchołkami. Byłoby to poprawne?
4 paź 15:03
henrys: tak

4 paź 15:04
PW: Właśnie to miałem pisać. Bez obliczeń, po prostu korzystamy z faktu, że przekątne kwadratu są
prostopadłe i połowią się.
4 paź 15:06
andy: 3•3+4•4=√c•c
c=√25
c=5
4 paź 15:22
andy: AC=2•5=10
4 paź 15:23
PW: andy, masz rację. Źle wyznaczyłem punkt symetryczny do (3, 4) − to powinien być (−3, −4),
i wtedy
d2 = (3+3)2 + (4+4)2 = 100.
Tak to jest gdy się samemu nie zrobi rysunku, tylko "w głowie". Dziękuję − zapis z 14:54
błędny!
4 paź 15:34


 Można skorzystać z wektorów
SA→ = [p, q]
SB→ = [−q, p]
SC→ = [−p, −q]
SD→ = [q, −p]
Można skorzystać z wektorów
SA→ = [p, q]
SB→ = [−q, p]
SC→ = [−p, −q]
SD→ = [q, −p]

 może ten rysunek Ci pomoże?
AC jest przekątną Twojego kwadratu, obracasz zielony trójkąt o 90. Wierzchołek A przejdzie na
kolejny wierzchołek kwadratu.
może ten rysunek Ci pomoże?
AC jest przekątną Twojego kwadratu, obracasz zielony trójkąt o 90. Wierzchołek A przejdzie na
kolejny wierzchołek kwadratu.
