Wyznacz wszystkie wartości parametru m
Zadaniowiec: witam, dobrze rozwiązuję et zadanie?
Wyznacz wszystkie wartości parametru m, dla których równanie x
2+(2m−5)x+2m+3=0 ma dwa różne
pierwiastki rzeczywiste x1, x2 takie, że (x1+x2)
2 ≥ x1
2*x2
2 ≥ x1
2+x2
2
Δ>0
Δ=4m
2−20m+25−8m−12
4m
2−28m+13>0
Δm=784−208=576
m1= 0,5 v m2=6,5
m∊ (−
∞, 0,5) v (6,5, +
∞)
x1+x2 = −2m+5
x1x2 = 2m+3
(x1+x2)
2 ≥ x1
2*x2
2 ≥ x1
2+x2
2
(−2m+5)
2 ≥ (x1*x2)
2 (x1*x2)
2 ≥ x1
2+x2
2
4m
2−20m+25 ≥ (2m+3)
2 (2m+3)
2 ≥ (x1+x2)
2−2x1x2
4m
2−20m+25 ≥ 4m
2+12m+9 4m
2+12m+9 ≥ (−2m+5)
2−2(2m+3)
−32m ≥ −16 /:(−16) 4m
2+12m+9 ≥
4m
2−20m+25−4m−6
2m ≥ 1 36m ≥ 10 /:2
m ≥ 0,5 18m ≥ 5 /:18
m∊ <0,5, +
∞) m ≥
518
m∊ <{5}{18}, +
∞)
dobrze tutaj wszystko wykonałem? jeżeli tak to jeszcze takie podstawowe pytanko, jak teraz ten
przedział dobrze wyznaczyć?
bo w założeniach delty wyszło m∊ (−
∞, 0,5) v (6,5, +
∞) i teraz w połączeniu z tymi to wyjdzie:
m∊<{5}{18}, 0,5)
to znaczy te przedziały co wyszły muszą się zgadać i zawierać w tych przedziałach z delty, tak?
przepraszam za tak oczywiste pytania, ale już chyba za długo przy tym dzisiaj siedzę i mi się
miesza
Zadaniowiec: tam wyżej mi się pomieszało trochę
oczywiście przy dzieleniu przez (−16) miała być zmiana znaku na 2m ≤ 1 i m ≤ 0,5
oraz ta linijka "4m2−20m+25−4m−6" powinna być tam na prawo przy tych działaniach, ale to pewnie
wiecie
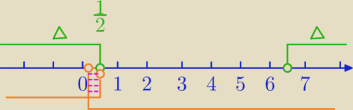1)Δ>0 na osi
i
2)
Warunek (1)
−32m≥−16 / (−32) zmieniamy kierunek nierówności