pomoc kirgo61: Witam, mam problem w zadaniu 5.23 (link) http://imageshack.com/a/img911/3713/Ouo0bM.jpg obliczyłem z tego delte i wyszła mi Δ=m²+4m. teraz pytanie jak działać dalej. z góry dziękuje za pomoc

ICSP: najmniejsza wartość funkcji kwadratowej to y_w

ICSP: Czyli u ciebie y_w będzie funkcją zmiennej m : y_w(m) = ... Masz znaleźć jej minimum.

kirgo61: tak ma być? http://imageshack.com/a/img901/8089/aDLJN4.jpg

ICSP: i teraz szukasz minimum.

kirgo61: jakaś wskazówka? od czego powinienem zacząć?

ICSP: gdzie funkcja kwadratowa przyjmuje swoje minimum bądź maksimum ?

kirgo61: na miejscach zerowych?

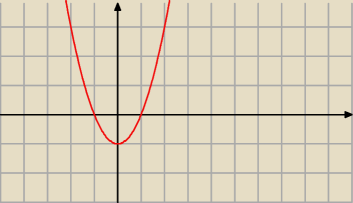
ICSP: najmniejsza wartość : dla jakiego argumentu jest przyjęta :

kirgo61: na −1?

ICSP: Powiedz mi co rozumiesz przez "na − 1" ?

kirgo61: −1 na osi OX.

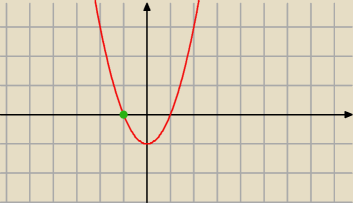
ICSP: czyli dla argumentu −1 wartość funkcji jest najmniejsza ? Nigdzie już parabola nie leży "niżej" ?

kirgo61: nie no, jest jeszcze niżej wierzchołek. czyli jak wcześniej było mówione y_w to najmniejsza wartość funkcji?

ICSP: y_w to najmniejsza albo największa wartość funkcji kwadratowej i ta wartośc jest przyjmowana dla argumentu : x_w. O tym czy jest to najwieksza czy najmniejsza wartość decyduje współczynnik a.

kirgo61: współczynnik a wynosi −1 (to co stoi przy x²)?

ICSP: : mamy funkcję f(x) = −x² + mx + m. Wiemy (a < 0) ży przyjmuje ona wartośc największa równą y_w. Jak na razie wykorzystujesz tylko podstawową wiedzę na temat funkcji kwadratowej.

	m2 + 4m
yw = ... =		= g(m)
	4

g(m) jest funkcją największych wartości f(x) w zależności od parametru m. Dalej polecenie mówi: "aby największa wartośc ... była najmniejsza z możliwych" Czyli musisz znaleźć takie m dla którego g(m) przyjmuje najmniejszą wartość.

kirgo61: ehh, najwyżej poszukam pomocy do rozwiązania na innym forum, ale dziękuje za próbę pomocy

kirgo61: oo

kirgo61: ok, wreszcie dałem radę dziękuje za pomoc