"wyznacz zbiór wartośći funkcji f, jeśli:" f(x)=-36^x-4*6^x-5 oraz f(x)=U{-2*5^x Anaka: Witam, czy ktoś może mi wyjasnic jak rozwiazac: "wyznacz zbiór wartośći funkcji f, jeśli:" f(x)=−36^x−4*6^x−5 oraz

	−2*5x−7
f(x)=
	5x−4

Proszę o pomoc :c wiem, że trzeba podstawić, tylko np w 1) wychodzi mi delta <0 a w drugim doszlam do

	1
f(x)=		− 2
	t−4

sushi_gg6397228:

1
	jak wygląda wykres funkcji ?
x

J: no i co z tego wynika,że : Δ < 0 ?

Anaka: 1/x to są hiperbole I własnie − co nam wynika z tego, że Δ<0

Anaka: Tzn że nie ma miejsc zerowych tylko co dalej

J: tzn .....przyjmuje tylko wartości ujemne

Anaka: Tzn no tak, a jaki kolejny krok?

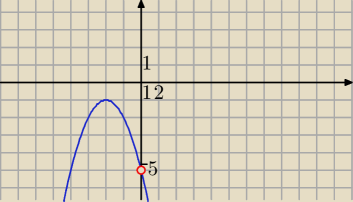
Mila: 1) f(x)=−36^x−4*6^x−5 f(x)=−6²x−4*6^x−5 6^x=t, t>0 f(t)=−t²−4t−5 , D=(0,∞) Parabola skierowana w dół t_w=−2 f(t) jest malejąca dla x>−2 f(0)=−5 Z_f=(−∞,−5)

Mila: Inny sposób: 2)

−2t−7
	=w
t−4

w− wartość funkcji t>0 i t≠4⇔ −2t−7=w*(t−4) −2t−7=w*t−4w −2t−w*t−7=−4w t*(−2−w)=−4w+7 Równanie ma rozwiązanie dla w≠−2

	−4w+7
t=
	−2−w

−4w+7
	>0⇔
−2−w

(−4w+7)*(−2−w)>0⇔

	7
w=		, w=−2
	4

	7
w<−2 lub w>
	4

	7
Zwf=(−∞,−2)∪(		,∞)
	4

Sprawdzić jeszcze jakie w dla t=4, czy nie trzeba czegoś wyrzucic z przedziałów.