równianie z modułem truskawka: Równanie ||x²−4|−1|=p ma dwa rozwiązania p ∊ ?

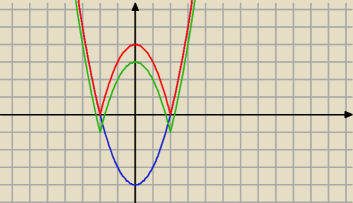
sushi_gg6397228: zacznij od wykresu y=x²−4

J: narysuj wykres: f(x) = IIx² − 4I − 1I ... i zobacz kiedy prosta: y = p przecina go w dwóch miejscach

sushi_gg6397228:

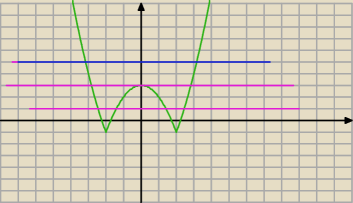
J: to jest: Ix² − 4I − 1 ... teraz odbij to co pod osią OX nad oś ... i odczytuj

J: widać: p > 3

truskawka: w odpowiedziach jest {−1} u (3;+∞) ale to nie może być chyba prawdą, bo wartość modułu nie może być ujemna, więc samo (3;+∞)?

sushi_gg6397228: obstawiam, że nie ma zewnętrznej wartości bezwzględnej y= |x²−4| −1

truskawka: jest, dobrze przepisałam wyjątkowo

truskawka: no czyli jest błąd w odpowiedziach, dzięki