Obszar pola
Pompon: Oblicz pole obszaru ograniczonego wykresami funkcji y=−x
2+3, y=2x−2 jak wyznaczyć
wogóle to pole, bo z wykresu niewiele wynika
2 paź 23:45
bezendu:
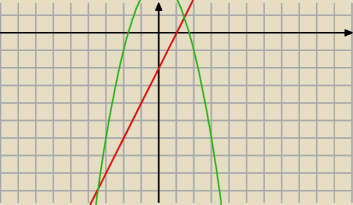
A ja widzę, że dużo wynika. Możesz ustalić obszar całkowania
Oblicz −x
2+3=2x−2 i masz punkt wspólne wykresu (początek i koniec obszaru całkowania)
2 paź 23:50
Pompon: | | 2−2√6 | | 2+2√6 | |
no to x1= |
| x2= |
| czy da się to jakoś uprościć? |
| | −2 | | −2 | |
2 paź 23:55
Qulka: √6−1 i −(√6+1)
2 paź 23:57
Pompon: jak obliczyć coś takiego (√6−1)3=?
3 paź 00:09
Pompon: czy trzeba stosować ten długi wzór na potęgę 3 stopnia?
3 paź 00:10
bezendu:
Całkować chcesz a wzorów skr. mnożenia nie umiesz zastosować ?
3 paź 00:16
Pompon: Czy pole tego obszaru jest równe 9? Bo tyle mi wyszło po długich męczarniach
3 paź 00:37
Qulka: do szacowania możesz policzyć kratki w środku ..zdecydowanie więcej niż 9
3 paź 00:43
Qulka: wynik to 8√6
3 paź 00:48
Pompon: no to zacznijmy od tego czy dobrze policzyłem całkę nieoznaczoną −13x3+3x−x2−2x+c?
3 paź 00:51
Pompon: podstawiam granice −√6−1√6−1
3 paź 00:54
Pompon: [−13(√6−1)3+3(√6−1)−(√6−1)2−2(√6−1)]−[−13(−√6−1)3+3(−
√6−1)−(−√6−1)2−2(−√6−1)]=
3 paź 00:58
Pompon: =[−3√6+7+3√6−3−7+2√6−2√6+1]−[3√6−5−3√6−3−6−2√6+1+2√6+2]=9
3 paź 01:01
Pompon: Jakby ktoś zerknął gdzie jest błąd byłbym wdzięczny
3 paź 01:01
Qulka: −(2x−2) = −x2+2x
3 paź 01:03
Pompon: dobra jutro będę męczył się jeszcze raz, bo już nie mam siły. Na razie dzięki
Qulka
3 paź 01:12
daras: jutro = dziś
3 paź 04:40