Nierówność z wartością bezwzględną
Janusz:
Rozwiąż:
x
16(3−x)
3(x
2+8)
3(x
3−x
2+x−1)
2<=0
A więc robię to tak:
x
16(3−x)
3(x
2+8)
3[(x
2+1)(x−1)]
2<=0
czyli naszymi pierwiastkami są:
0 − parzystokrotne
3 − nieparzystokrotne
1 − parzystokrotne
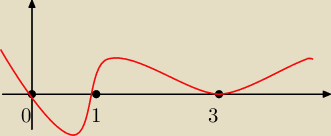
A więc szkicuję wykres (rysunek)
Z wykresu mi wychodzi, że rozwiązaniem jest:
x∊<0;1> U {3}
Według wolframa jest to zakres <3;+
∞)
ktoś, coś?
2 paź 21:33
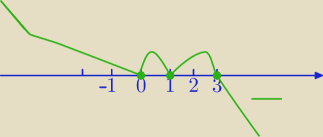
sushi_gg6397228:
parzyste= odbija
nieparzyste= przechodzi
na wykresie masz odwrotnie
2 paź 21:38
PW: Źle narysowałeś wykres. Mówisz o parzystości, a rysujesz inaczej. Na przykład przy przejściu
przez 0 znak nie zmienia się, bo jest x16 − z lewej i z prawej strony zera x16 jest
dodatnie.
2 paź 21:40
===:
...sprawdź jaka krotność "odbija"

2 paź 21:40
Janusz: Ehh... faktycznie
ale to i tak sie nie zgadza, bo będzie:
x∊{0,1} U <3, +∞)
2 paź 21:41
Janusz: Może źle w wolframie cos wpisalem.
Taki wynik jest poprawny?
2 paź 21:42
sushi_gg6397228:
zalezy co wpisałeś do wolframa− ułamek czy wielomian?
2 paź 21:43
Janusz: Dobra mam. Za dużo chyba na dziś, skoro na takich podstawach się mylę...
Dziękuję wszystkim za pomoc, pozdrawiam!

2 paź 21:46
Mila:
x
16(3−x)
3*(x
2+8)
3*(x
3−x
2+x−1)2≤0⇔
x
16(3−x)
3*(x
2+8)
3*[(x
2(x−1)+(x−1)]
2≤0⇔x
16(3−x)
3*(x
2+8)
3*(x−1)
2*(x
2+1)
2≤0
⇔x
16(3−x)
3*(x−1)
2*≤0 [x
2+8>8, x
2+1>0]
x=0 parzysta potęga
x=3 − nieparzysta potęga
x=1 − parzysta potęga
Stopień wielomianu ( z ostatniej nierówności): 16+3+2=21
x∊<3,
∞)U{0,1}
2 paź 21:47
Janusz: Dziękuję Mila!

2 paź 21:50
Mila:

2 paź 22:25
 Rozwiąż:
x16(3−x)3(x2+8)3(x3−x2+x−1)2<=0
A więc robię to tak:
x16(3−x)3(x2+8)3[(x2+1)(x−1)]2<=0
czyli naszymi pierwiastkami są:
0 − parzystokrotne
3 − nieparzystokrotne
1 − parzystokrotne
A więc szkicuję wykres (rysunek)
Z wykresu mi wychodzi, że rozwiązaniem jest:
x∊<0;1> U {3}
Według wolframa jest to zakres <3;+∞)
ktoś, coś?
Rozwiąż:
x16(3−x)3(x2+8)3(x3−x2+x−1)2<=0
A więc robię to tak:
x16(3−x)3(x2+8)3[(x2+1)(x−1)]2<=0
czyli naszymi pierwiastkami są:
0 − parzystokrotne
3 − nieparzystokrotne
1 − parzystokrotne
A więc szkicuję wykres (rysunek)
Z wykresu mi wychodzi, że rozwiązaniem jest:
x∊<0;1> U {3}
Według wolframa jest to zakres <3;+∞)
ktoś, coś?


 x16(3−x)3*(x2+8)3*(x3−x2+x−1)2≤0⇔
x16(3−x)3*(x2+8)3*[(x2(x−1)+(x−1)]2≤0⇔x16(3−x)3*(x2+8)3*(x−1)2*(x2+1)2≤0
⇔x16(3−x)3*(x−1)2*≤0 [x2+8>8, x2+1>0]
x=0 parzysta potęga
x=3 − nieparzysta potęga
x=1 − parzysta potęga
Stopień wielomianu ( z ostatniej nierówności): 16+3+2=21
x∊<3,∞)U{0,1}
x16(3−x)3*(x2+8)3*(x3−x2+x−1)2≤0⇔
x16(3−x)3*(x2+8)3*[(x2(x−1)+(x−1)]2≤0⇔x16(3−x)3*(x2+8)3*(x−1)2*(x2+1)2≤0
⇔x16(3−x)3*(x−1)2*≤0 [x2+8>8, x2+1>0]
x=0 parzysta potęga
x=3 − nieparzysta potęga
x=1 − parzysta potęga
Stopień wielomianu ( z ostatniej nierówności): 16+3+2=21
x∊<3,∞)U{0,1}

