Wykaż, że Maciek:

	4		3		1
Wykaż, że jeśli A,B⊂Ω i P(A)<		; P(A∩B)>		to P(A∩B')<
	7		8		5

sushi_gg6397228: zrób rysunek

Maciek: Zrobiłem, zapisałem równość P(A)=P(A∩B')+P(A∩B), ale nie wiem co dalej.

sushi_gg6397228: nie widze

Maciek: No w zeszycie zrobiłem

sushi_gg6397228: rysuj tutaj

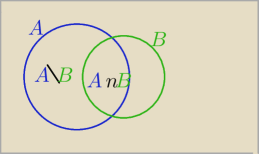Eta: A∩B^'= A\B= A \( A∩B)

	4		3		11		1
P(A∩B')= P(A)− P(A∩B)=		−		=		<
	7		8		56		5

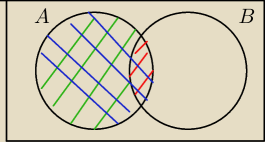Maciek: Czerwony to A∩B, zielony to A∩B', a niebieski to A.

Maciek:

	4		3
Dobra, poukładałem sobie w głowie, czemu można po prostu sobie odjąć		od		.
	7		8

Szukamy największej wartości, więc żeby to osiągnąć wstawiamy za P(A) największą możliwą liczbę, a za P(A∩B) najmniejszą możliwą liczbę, wtedy otrzymana różnica pokaże największą wartość P(A∩B'), czyli w rezultacie od czego jest mniejsza. Dzięki!

Maciek: Mam problem z następnym zadaniem, bardzo podobnym.

	1		1		1		7		1
Wykaż, że jeśli P(A)=		; P(B)=		to		≤ P(A∪B) ≤		oraz P(A∩B) ≤
	4		2		3		12		4

	7		1
Nie mam pojęcia jak mają wyjść liczby:		i		. Załóżmy P(A∩B)=∅ to wtedy
	12		3

	3		3		7		7
P(A∪B)=		, a		>		, co ogranicza to prawdopodobieństwo do liczby		?
	4		4		12		12

:):

	1
Chyba mialo byc P(B)=
	3

	1
P(A∩B)=P(A)+P(B)−P(A∩B)≥P(B)≥		, bo P(A∩B)≤P(A)
	3

	1		1		3		4		7
P(A∩B)≤P(A)+P(B)=		+		=		+		=
	4		3		12		12		12

:):

	1
A∩B⊂A wieć P(A∩B)≤P(A)=
	4

Maciek: Dzięki wielkie !